We are going to introduce the concepts of Position, distance and displacement in this lesson.
• Define position, displacement, distance, and distance traveled.
• Explain the relationship between position and displacement.
• Distinguish between displacement and distance traveled.
• Calculate displacement and distance given initial position, final position, and the path between the two.

In order to describe the motion of an object, you must first be able to describe its position—where it is at any particular time. More precisely, you need to specify its position relative to a convenient reference frame. Earth is often used as a reference frame, and we often describe the position of an object as it relates to stationary objects in that reference frame. For example, a rocket launch would be described in terms of the position of the rocket with respect to the Earth as a whole, while a professor’s position could be described in terms of where she is in relation to the nearby white board. (See Figure 2.3.) In other cases, we use reference frames that are not stationary but are in motion relative to the Earth. To describe the position of a person in an airplane, for example, we use the airplane, not the Earth, as the reference frame. (See Figure 2.4.)
If an object moves relative to a reference frame (for example, if a professor moves to the right relative to a white board or a passenger moves toward the rear of an airplane), then the object’s position changes. This change in position is known as displacement. The word “displacement” implies that an object has moved, or has been displaced.
Displacement
Displacement is the change in position of an object:
Δx = xf − x0, (2.1)
where Δx is displacement, xf is the final position, and x0 is the initial position.
In this text the upper case Greek letter Δ (delta) always means “change in” whatever quantity follows it; thus,
Δx means change in position.
Always solve for displacement by subtracting initial position x0 from final position xf .
Note that the SI unit for displacement is the meter (m) (see Physical Quantities and Units), but sometimes kilometers, miles, feet, and other units of length are used. Keep in mind that when units other than the meter are used in a problem, you may need to convert them into meters to complete the calculation.
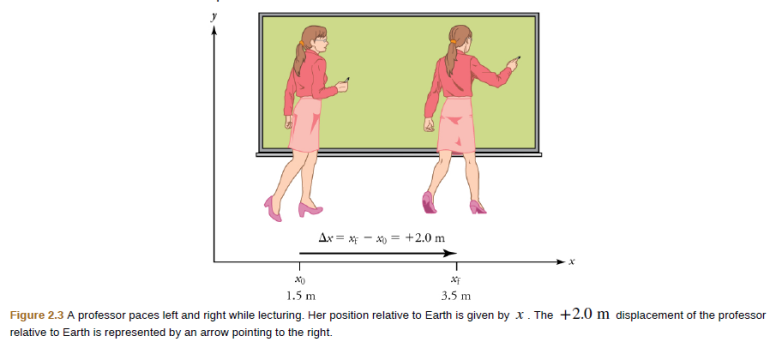
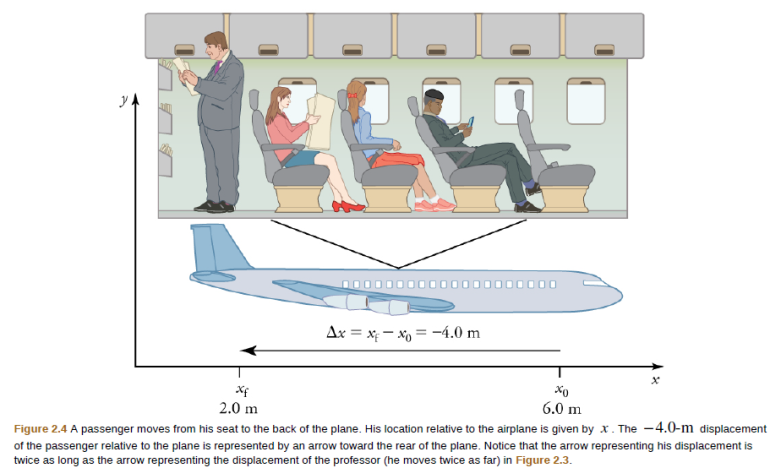
Note that displacement has a direction as well as a magnitude. The professor’s displacement is 2.0 m to the right, and the airline passenger’s displacement is 4.0 m toward the rear. In one-dimensional motion, direction can be specified with a plus or minus sign. When you begin a problem, you should select which direction is positive (usually that will be to the right or up, but you are free to select positive as being any direction).
The professor’s initial position is x0 = 1.5 m and her final position is
xf = 3.5 m .
Thus her displacement is
Δx = xf −x0 = 3.5 m − 1.5 m = + 2.0 m. (2.2)
In this coordinate system, motion to the right is positive, whereas motion to the left is negative. Similarly, the airplane passenger’s initial position is x0 = 6.0 m and his final position is xf = 2.0 m , so his displacement is
Δx = xf −x0 = 2.0 m − 6.0 m = −4.0 m. (2.3)
His displacement is negative because his motion is toward the rear of the plane, or in the negative x direction in our coordinate system.
Although displacement is described in terms of direction, distance is not. Distance is defined to be the magnitude or size of displacement between two positions. Note that the distance between two positions is not the same as the distance traveled between them. Distance traveled is the total length of the path traveled between two positions. Distance has no direction and, thus, no sign. For example, the distance the professor walks is 2.0 m. The distance the airplane passenger walks is 4.0 m.