The speed of an object is a measure of how fast something is traveling.
speed (m/s) = distance (m) ÷ time (s)
Alternatively the units are kilometers per hour (km/h).
You will also see miles and miles per hour:
Despite this country’s love of imperial distance measurements, all Highways and many main roads have distance markers in kilometers.
Most modern engineering is done entirely metrically, and has been for many years.
The equation can be rearranged to:
distance = speed × time
or
time taken = distance ÷ time
OR:
This is the separation or space between two points. It is measured in meters and it is a scalar quantity.
It is distance in a specified direction. It is a vector quantity and it is measured in meters.
It is the rate of change of distance moved with time. The unit is m/ and it is a scalar quantity.
Speed=distancetimev=st
It is obtained if the rate of change of distance with time is constant or when a body travels equal distances in equal time intervals.
Average speed is the total distance travelled divided by the total time taken. The average speed is a better representation of the motion of a body not moving at a constant or uniform speed.
Average speed=Total distance coveredTotal time taken
It is the actual speed of a body at any instant during the course of motion.
It is the rate of change of displacement with time. The unit is m/s. It is avector quantity.
Velocity=displacementtime
It occurs when the rate of change of displacement with
time is constant or when a body travels equal displacement in equal time interval.
EVALUATION
A car covers a distance of 60km in half an hour. What is the average speed of the car in (a) km/hr (b) m/s
Solution:
(a) Time = ½ hour = 0.5 hour =12hour=0.5hour
Average speed=Total distance coveredTotal time taken=600.5=120km/h
(b) Convert km/hr to m/s
1km/h=100060×60m/s1km=1000m1hr=3600s120km/h=120×100060×60=33.33m/s
A car travelled to Lagos a distance of 150m in 100 seconds. Calculate his average speed.
Solution:
Average speed=Total distance coveredTotal time taken=150100=1.5m/s
A car covers 1500m in 10 secs. What is the speed in km/hr?
Solution:
Speed=distancetime=150010=150m/s
Convert to km/hr
1km/h=100060×60m/s1m/s=60×601000km/h150m/s=150×60×601000=540km/h
EVALUATION:
Convert 144km/h to m/s.
A car covers a distance of 40m in 2 sec. What is his speed in km/h?
It is the graphical representation of the motion of a body. There are Distance-time graph, Displacement-time graph and Velocity-time graph.
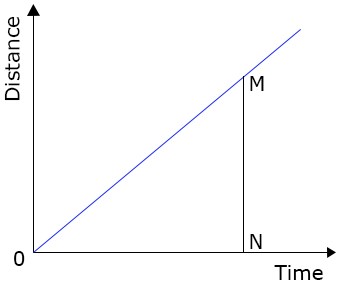
Slope of distance–time graph = speed
When an object increases or changes its velocity within a set time, the object is said to undergo acceleration (or to accelerate). We therefore define acceleration as the rate of change of velocity with time.
Acceleration=Change in VelocityTime takena=v–ut
Where a: acceleration
v: final velocity
u: initial velocity
Acceleration is a vector quantity and its SI unit is m/s2
However, be reminded that:
(i) When a body starts from rest, its initial velocity, ‘u’ is zero.
(ii) When a body comes to rest, its final velocity, ‘v’ is zero.
Acceleration is said to be uniform if the velocity increases by equal amounts in equal intervals of time. That is, the time rate of change of velocity is constant. If the rate of change of velocity with time is not constant, then, the acceleration is non-uniform.
Deceleration is defined as a negative change in velocity with time. When such happens, the body’s velocity is said to be reducing or coming to rest.
Deceleration is said to be uniform if the velocity decreases by equal amounts in equal intervals of time. That is, the negative change in velocity with time is constant.
Also, Deceleration=Change in VelocityTime taken=v–ut
Deceleration is also called retardation and its SI unit is m/s2. It is also a vector quantity.
EVALUATION
Example 1: A body experienced a change in velocity of 10m/s in 15s. What is the acceleration of the body?
Solution:
Data: ∆v = 10m/s, t = 15s, a = ?
Now, a=ΔvΔt=1015=0.67m/s2
Example 2: A car accelerated uniformly at 6m/s2 in 20s. What was the change in velocity?
Solution:
Data: a = 6m/s2, t = 20s, ∆v = ?
Now, a=ΔvΔtΔv=a×ΔtΔv=6×20Δv=120m/s
Example 3: The velocity of a lorry decreased from 60km/h to 35km/h within 0.5mins. Find the deceleration.
Solution:
Data: u=60kmh=60×100060×60=60003600=16.67m/s,v=35km/h=9.72m/s,t=0.5mins=30s,d=?
Now, d=ΔvΔt=v–ut=9.72–16.6730=−6.9530d=−0.23m/s2
The negative sign shows that it is decelerating thus coming to rest.
( NOTE: you can convert velocity in km/h to m/s by simply dividing by 3.6 )
EVALUATION
EVALUATION
N.B: for bodies moving with constant or uniform acceleration, the following formulas could be used.
v=u+at… … … (i)
s=ut+12at2… … … (ii)
s=(v+u2)t… … … (iii)
v2=u2+2as … … … (iv)
Solution:
1st stage data: u = 0 (because it started fron rest); a = 2m/s2, t = 20s; v = ?
2nd stage data: u = value of ‘v’ above; v = 0 (because it came to rest); t = 10s
∴ v=0+2×20=0+40
∴ v=40m/s
In the first stage, using v2=u2+2as
∴ s =v2–u22a=402–02×2=16004=400m
In the second stage, using v2=u2+2as
Here, “a” is deceleration and not acceleration. We need to find it.
Deceleration =v–ut=0–4010=−4m/s2
∴ s=v2–u22a=0–4022×−4=−1600−8=200m
∴ Total distance travelled =400m+200m=600m
(NB: You can also use s=ut+12at2 for each stage)
Find the value of x
Find the distance travelled during the acceleration and the deceleration.
Find the total distance travelled.
Solution:
1st stage data: u = 0 (Because it started from rest); a = xm/s2; v = 60m/s, t = 23s.
2nd stage data: u = 60m/s; v = 0 (because it came to rest); t = 15s
∴ x=2.61m/s2
s=v2–u22a=602–02×2.61=36005.22=689.6m=690m
Now, the deceleration =v–ut=0–6015=−4m/s2
Now, s=v2–u22a=0–6022×−4=−3600−8=450m
Total distance travelled =690m+450m=1,140m.
E=MC2
Speed, Distance and Time
| Name | Time taken (s) |
| Jenny | 15 |
| Ahmed | 12 |
| Kevin | 13 |
| Julia | 12 |
| Louise | 16 |
Read our disclaimer.
AD: Take Free online baptism course: Preachi.com 