Gaseous state and gas laws II

KINETIC THEORY OF  GASES

The kinetic theory of matter postulates that the tiny Particles of matter are continually moving and so possess kinetic energy. An increase in temperature causes an increase in the average kinetic energy of the particle.

Dalton’s experimental evidence shows that chemical compounds consists of molecules, which are groups of atoms of various elements. The gas laws which explained the physical behaviour of gases can be explained by kinetic theory of gases. This theory describes the behaviour of an ideal or perfect gas. This is to say that the kinetic theory of gases explains quantitatively the properties of gas molecules and in so doing put up the following assumptions.

1. A gas consists of very tiny particles (usually molecules and atoms).
2. The cohesive forces of the gas molecules are negligible.
3. These particles are in constant random and rapid motion in straight lines.
4. As a result of these movements, collisions occur between the molecules and also with the walls of the container, hence the molecules exert pressure. No energy is lost when collision occupy. This means that the collisions are perfectly elastic.
5. The space between the molecules is very large compared to the size of the molecules. The molecules therefore have negligible (almost zero) volume compared to the volume of the container.
6. The average kinetic energy per molecule is the same for all gas samples at any given temperature. The absolute temperature of the gas is a measure of the average kinetic energy of the gas particles.

EVALUATION

1. The kinetic theory of matter postulates ……………………..
2. When the temperature of the particles of the molecules increases, what happens to kinetic energy?
3. Enumerate the six assumptions if the kinetic theory of matter.

THE APPLICATION OF KINETIC THEORY

The kinetic theory is useful in several respects and such aspects includes;

1. It provides reasonable explanations for the behaviour of gas.
2. It accounts for the gas laws
3. It explains important phenomenon such as diffusion
4. It provides a fundamental equation for gases.

PV=13NMC2

EVALUATION

1. Mention four applications of kinetic theory of matter.

PHENOMENA TO ILLUSTRATE THE KINETIC THEORY OF MATTER

The following phenomena illustrate the kinetic theory of matter

1. Dispersion
2. Evaporation
3. Diffusion:
4. Brownian motion
5. Osmosis
6. Tyndall effect
7. Effusion

EVALUATION

1. Define the term matter.
2. State the three state of matter.
3. Explain two out of the three main sate of matter.
4. List four importance of kinetic theory.
5. Give assumptions of kinetic theory of matter.

BOYLE’S LAW

The relationship between volume and pressure of a gas was first started by Robert Boyle in 1662.

Boyle’s law states that the volume of a given mass of gas is inversely proportional to its pressure, provided that the temperature remains constant.

According to Boyle’s law, volume of a gas increases as the pressure decreases and vice versa.

This relationship is independent of the nature of the gas and it can be expressed mathematically as:

V∝1P∴V=kp

or PV=k

Where V = Volume at pressure P

K = A mathematical constant

For a given mass of a gas, the product of its pressure and its volume is always a constant. If the pressure of a given mass of gas increases, its volume will decrease by a similar proportion and vice versa, as long as the temperature remain constant. This relationship can also be expressed mathematically as:

P1V1=P2V2

Where V₁ = Volume at pressure P₁

V₂ = Volume at pressure P₂

Boyle’s law can still be re-stated as: ‘The pressure of a given mass of gas is inversely proportional to its volume, provided the temperature remains constant. Boyle’s law can further be illustrated with the diagram below, showing that when P is increasing, V is decreasing and when P is decreasing, V is increasing.

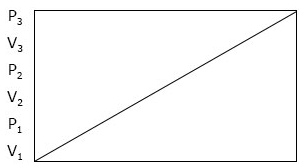
P₁ = Initial pressure

P₂ = Final pressure

V₁ =Initial volume

V₂ = final volume

Graphical representation of Boyle’s law

Graphical Representation of Boyles Law

Worked examples

1. 375cm³of a gas has a pressure of 770mmHg. Find its volume if the pressure is reduced to 750mmHg.

P1V1=P2V2 (Boyle’s law)

P₁ = 770mmHg

P₂ = 750mmHg

V₁= 375cm3

V₂ = ?  (new volume of gas)

P1V1=P2V2V2=P1V1P2=770×375750=385cm3

The new volume will be 385cm³

100cm³ of a gas has pressure of 1 atmosphere. Determine the volume of the gas at 5 atmospheres keeping the temperature constant.

Solution: since T is constant, we are to use Boyle’s law.

P₁  Initial pressure = l atmosphere

P₁ Final pressure = 5

V₁  Initial volume = 100cm³

V₂ (required quantity)

Recall: V2=P1V1=P2V2

V2=P1V1P2=100×15=20cm3

EVALUATION:

1. A given quantity of gas occupies a volume of 228cm³at a pressure of 750mmHg. What will be its at atmospheric pressure if temperature is kept constant?
2. A given mass of gas at 55⁰C has a pressure of 3.6 x 10⁴Nm^-2and occupies a volume of 1.8dm3. What volume will it occupy if its pressure is increased to 4.8 x 10⁴Nm^-2 if the temperature is kept constant?

CHARLES’ LAW

The effect of temperature changes on the volume of a given mass of a gas at a constant pressure is described by Charles. Charles’ law states that the volume of a given mass of gas is directly proportional to its temperature in Kelvin, provided that pressure remains constant.

The volume of the gas decreases as the temperature decreases, and increases as the temperature increases.

Mathematically, the law can be expressed as:

V∝T∴V=kT

or VT=k

Where V = volume

T = Kelvin Temperature

K = mathematical constant

A Representation of Charles’s law

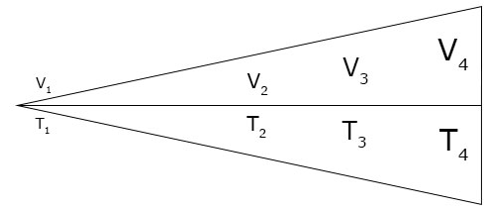
For a direct relationship, when the temperature increases, the volume will also increase at the same rate and vice versa, at constant pressure .The diagram above shows that when V is decreasing, T is also decreasing and when V is increasing, T is also increasing thus, making the quotient constant.

Charles’s law can be represented graphically has shown below.

If we divide the varying gas volumes by the corresponding temperature in Kelvin, the result would always be a constant. This relationship can also be expressed in another form.

V1T1=V2T2∴V2=T2V1T1

Where V₁ is the volume at temperature T₁

V₂ is the volume at temperature T₂

ABSOLUTE ZERO

This is the temperature at which the volume of a gas is theoretically zero..At this temperature there is no motiom of any form and all gases have been liquefied or solidified. The value of the temperature is -273⁰C.

TEMPERATURE CONVERSION

1. To convert from Celsius scale to Kelvin scale, add 273 i.e. T = ⁰C + 273. This is because O⁰C = 273K.
2. To convert from Kelvin scale to Celsius scale, subtract 273. i.e ⁰C = T − 273.

Where T = Temperature in Kevin

⁰C = Temperature in Celsius.

Examples:

1. Convert the following Celsius temperature to Kelvin temperature.

(a) 100⁰C (b) 0⁰C (c) -570C

Solution

Recall: T = 0C + 273

(a) 100⁰C = (100 + 273) = 373k

0C =(0 + 273) = (0 + 273) = 373k

(b) −57⁰c = (−57 + 273)k = (273 − 57) = 216k

2. Convert the following Kelvin temperatures to Celsius temperature.

(a) 298k (b) 405k (b) 285k (d) 0k

Solution

Recall 0⁰c = k – 273

298k = (298 – 273)⁰C = 25⁰C

405k = (405 – 273)⁰C = 12⁰C

0k = (0 – 273)⁰C = − 273⁰C

Worked examples on Charles’s law

1. A gas occupies a volume of 20.0dm³at 373k. Its volume at 746k at that pressure will be?

Here pressure is constant. Charles’s law will apply.

V₁ = 20.0dm³

T₁ = 273k

T₂ = 746

Recall Charles’s law V1T1=V2T2V2=T2V1T1V2=20×746273=40.0dm3

EVALUATION:

1. State Charles’s law
2. Express the two laws mathematically
3. Draw two graphs to illustrate Charles’ law.

post your answers to the forum for review