Arc length of a sector, Area of a sector

Arc length of a sector

If you take a part of the circumference of a circle then the distance along this arc is called the arc length. So since the arc length is part of the circumference of a circle, then the arc length of the sector can be found by using the following formula:

L = (θ/360) × π × d

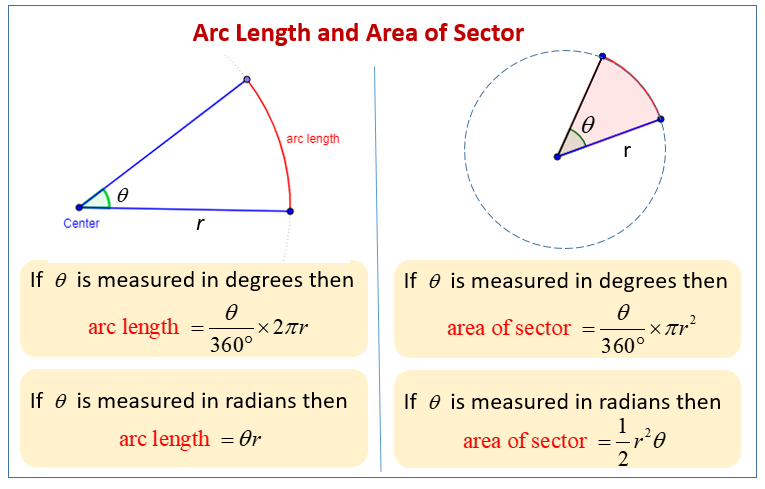
Where L is the arc length, θ is the angle inside the sector and d is the diameter of the sector.

So make sure that you use the diameter of the circle if you are calculating the arc length of a sector.

The angle inside the sector is 41⁰, so x = 41⁰.

Now the diameter of the whole circle is 24cm (as the 12cm is the radius), so d = 24cm.

All you need to do now is substitute these values into the above formula so you can find the arc length.

l = (x/360) × π × d

L = (41/360) × π × 24

L = 8.6 cm rounded to 1 decimal place.

Area Of a Sector

You can work out the Area of a sector by comprising its angle to the angle of a full circle.

Note: I am using radians for the angles. This is the reasoning.

So a Sector with an angle of θ (instead of 2π) must have an area of: (θ/2π) × πr²

Which can be simplified to: (θ/2) × r²

Area of Sector = ½ × θ × r²   (when θ is in radians)

Area of Sector = ½ × (θ × π/180) × r²   (when θ is in degrees)