What are Trigonometric Ratios?
Trigonometry is the study of triangles in relation to their sides and angles and many other areas which find applications in many disciplines. In particular, trigonometry functions have come to play great roles in science. For example, in physics, it is used when we want to analyse different kinds of waves, like the sound waves, radio waves, light waves, etc. Also trigonometric ideas are of great importance to surveying, navigation and engineering.
We shall, however at this stage be concerned with the elementary ideas of trigonometry and their application.
The basic trigonometric ratios are defined in terms of the sides of a right-angled triangle. It is necessary to recall that in a right-angled ∆ABC, with LC = 900, the side AB opposite the 900 is called the hypotenuse.
The notion that there should be some standard correspondence between the lengths of the sides of a triangle and the angles of the triangle comes as soon as one recognizes that similar triangles maintain the same ratios between their sides. That is, for any similar triangle the ratio of the hypotenuse (for example) and another of the sides remains the same. If the hypotenuse is twice as long, so are the sides. It is these ratios that the trigonometric functions express.
To define the trigonometric functions for the angle A, start with any right triangle that contains the angle A. The three sides of the triangle are named as follows:
In ordinary Euclidean geometry, according to the triangle postulate, the inside angles of every triangle total 180o (π radians). Therefore, in a right-angled triangle, the two non-right angles total 90° (π/2 radians), so each of these angles must be in the range of (0°, 90°) as expressed in interval notation. The following definitions apply to angles in this 0° – 90° range. They can be extended to the full set of real arguments by using the unit circle, or by requiring certain symmetries and that they be periodic functions. For example, the figure shows sin θ for angles θ, π − θ, π + θ, and 2π − θ depicted on the unit circle (top) and as a graph (bottom). The value of the sine repeats itself apart from sign in all four quadrants, and if the range of θ is extended to additional rotations, this behavior repeats periodically with a period 2π.
Rigorously, in metric space, one should express angle, defined as scaled arc length, as a function of triangle sides. It leads to inverse trigonometric functions first and usual trigonometric functions can be defined by inverting them back.
The trigonometric functions are summarized in the following table and described in more detail below. The angle θ is the angle between the hypotenuse and the adjacent line – the angle at A in the accompanying diagram.
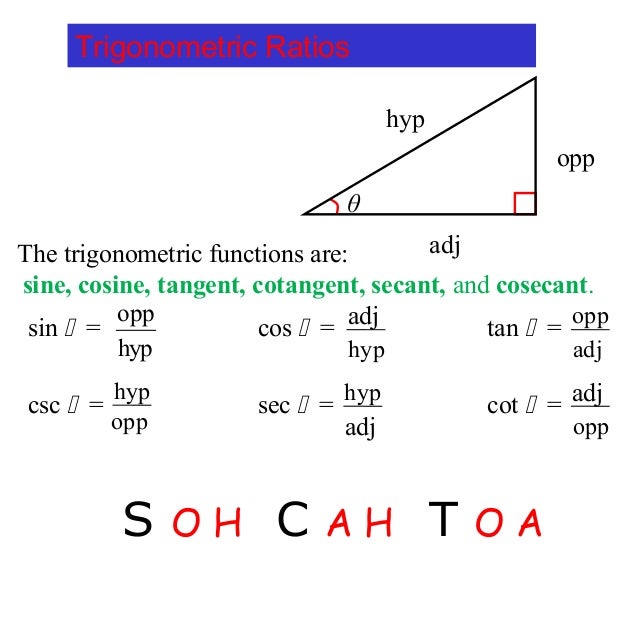
| Function | Abbreviation | Description | Identities (using radians) |
| Sine | sin | opp/hyp | sin θ = (π/2 – θ) = 1/csc θ |
| Cosine | cos | adj/hyp | cos θ = (π/2 – θ) = 1/sec θ |
| Tangent | tan | opp/adj | tan θ = (sin θ/cos θ = cot (π/2 – θ) = 1/cot θ |
| Cotangent | cot | adj/opp | cot θ = cos θ/sin θ = tan (π/2 – θ) = 1/tan θ |
| Secant | sec | hyp/adj | sec θ = csc (π/2 – θ) = 1/cos θ |
| Cosecant | cosec | hyp/opp | csc θ = sec (π/2 – θ) = 1/sinθ |
Read our disclaimer.
AD: Take Free online baptism course: Preachi.com 