CONTENT
Heat is a form of energy that moves from one point to the other due to temperature difference. When you dip one end of an iron rod into fire and hold the other end with your hand, this other end soon becomes hot because energy has flowed from the point dipped into the fire to this other end. This energy flow is what is known as heat. Temperature is a measure of how cold or hot a body is.
| S/N | Heat | Temperature | |
| 1 | It is a form of energy | It is not a form of energy | |
| 2 | It is measured in joules | It is measured in Kelvin | |
| 3 | It is a form of energy transferred from body at a higher temperature to one at a lower temperature | It is a measure of the average kinetic energy of the constituent particle of the a substance | |
| 4 | It is a derived quantity | It is a fundamental quantity | |
| 5 | Other unit for measuring heat: calorie (Cal), kcal, … | Other units include: 0F, 0C | |
| 6 | It can be determined using a calorimeter | It can be measued using a thermometer | |
The kinetic theory of matter states that:
EVALUATION
When heat is applied to a substance, it can lead to the following changes
Most solid substances expand when heated. The rate of expansion varies from one solid to another. Expansion is more pronounced in gases followed by liquids and least in solids. A substance whether solid, liquid or gaseous consists of molecules. When the substance is heated, the molecules gain kinetic energy and move faster and hence the molecules take up more space in the substance. This leads to expansion.
Experiment to demonstrate expansion of a solid.
Apparatus: Bunsen burner, ball and ring apparatus
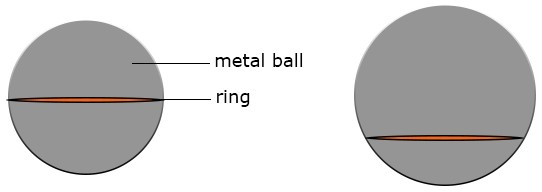
Procedure: Allow the metal ball to pass through the ring. Heat the metal ball for some time in the Bunsen burner and make it pass through the same ring. The metal ball will no longer pass through the same ring it passed through earlier as a result of expansion. When allowed to cool down for some time and allowed to pass through the ring once more, it will pass through because it has contracted and regained its original size.
According to the kinetic theory of matter, the average kinetic energy of the molecules is directly proportional to the temperature. This means that as the kinetic energy of the molecules increases, the temperature also increases. When a body is subjected to heat, the velocities of the molecules increases and hence they gain more kinetic energy this of course will lead to increase in the temperature of the body. On the other hand, if we reduce or lower the heat, the velocities of the molecules will decrease leading to a decrease in the kinetic energy of the molecules. Hence the temperature falls or reduces.
EVALUATION
Linear expansion is expansion in length of a body. Different solids expand at different rates, this is because they have different coefficient of linear expansivity.
It is defined as increase in length per unit length per degree rise in temperature. The unit is per Kelvin or 1/K or K–1
α=Increase in lengthoriginal length×temperature rise=L2–L1L1(θ2–θ1)
L2 – L1 = Increase in length or expansion
θ2 – θ1 = Temperature rise or increase in temperature
θ2 is final temperature
θ1 is initial temperature
L2 is new length
L1 is original length
Question 1.
What is meant by the statement, the linear expansivity of copper is 0.000017/k?
Solution:
It means that the increase in length per unit length per degree rise in temperature of copper is 0.000017m.
Question 2.
A brass is 2 meters long at a certain temperature. What is its length for a temperature rise of 100k, if expansivity of brass is 1.8 x 10-5/k
α =Increase in lengthoriginal length×temperature rise=L2–L1L1(θ2–θ1)
L2–L1=αL1(θ2–θ1)L2=L1{α(θ2–θ1)+1}L2=2{1.8×10−5(100)+1}L2=2{0.0018+1}L2=0.0036+2=2.0036m
Question 3.
A metal of length 15.01m is heated until its temperature rises to 600C. If its new length is 15.05m, calculate its linear expansivity.
Solution:
L1 = 15.01m, L2 = 15.05, θ2 – θ1 = 60o, L2 – L1 = 0.04
α=Increase in lengthoriginal length×temperature rise=L2–L1L1(θ2–θ1)α=15.05–15.0115.01×60o=0.04900.6=0.000044=4.4×10−5/k
EVALUATION
Apparatus: Thermometer, Micrometer screw gauge, steam jacket, metal rod, meter rule
Method:
(i) Measure the length of the metal rod (L1).
(ii) Insert the metal rod in the steam jacket and take the initial temperature of the metal rod with thermometer (θ1).
(iii) Screw the micro-meter to touch the end of the rod and take the reading of micro-meter (xi).
(iv) Unscrew micro meter to make room for expansion of metal rod.
(v) Introduce steam into the steam jacket for several minutes then the metal rod will expand.
(vi) Screw the micrometer screw guage to touch the end of the metal rod again and take the reading again (x2).
(vii) Record the final temperature (θ2).
Calculation:
α=x2–x1x1(θ2–θ1)
Conclusion: Since all parameters are known, α can be calculated
It is defined as the increase in area per unit area per degree rise in temperature
β=Increase in Areaoriginal area×temperature rise=A2–A1A1(θ2–θ1)
A2 – A1 = Increase in area or expansion
θ2 – θ1 = Temperature rise or increase in temperature
θ2 is final temperature
θ1 is initial temperature
A2 is new area
A1 is original area
Question 1: A metal cube of cross sectional area 3.45m2 at 00C is heated at a temperature rise of 70K, when the final length of the cube is 3m. Find the:
(i) coefficient of superficial expansivity.
(ii) coefficient of linear expansivity.
Solution
(i) β=Increase in Areaoriginal area×temperature rise=A2–A1A1(θ2–θ1)A2=L2=3×3=9m2θ2–θ1=70kA1=3.45m2β=9–3.453.45×70=5.55241.5=0.023/k=2.3×10−2/k
(ii) β=2αα=β2α=2.3×10−22=1.15×10−2K−1
EVALUATION
It is defined as the increase in volume per unit volume per degree rise in temperature
γ=Increase in Volumeoriginal volume×temperature rise=V2–V1V1(θ2–θ1)
V2 – V1 = Increase in volume or expansion
θ2 – θ1 = Temperature rise or increase in temperature
θ2 is final temperature
θ1 is initial temperature
V2 is final volume
V1 is original volume
Question 2: The increase in the volume of 10cm3 of mercury when the temperature rises by 1000C is 0.182cm3. What is cubic expansivity of mercury.
γ=Increase in Volumeoriginal volume×temperature rise=V2–V1V1(θ2–θ1)
V2 – V1 = Increase in volume = 0.182cm2
θ2 – θ1 = Temperature rise = 100oC
V1 = original volume = 10cm2
γ=0.18210×100=0.1821000=0.00082/k=1.82×10−4K−1
Expansion in liquid is complicated by the expansion of the container because while the liquid expands, the container equally expands. So it is important to differentiate between real and apparent cubic expansivity.
Real or Absolute Cubic Expansivity (γr):
It is defined as the increase in volume per unit volume per degree rise in temperature.
Apparent Cubic Expansivity (γa):
It is defined as the increase in volume per unit volume per degree rise in temperature when the liquid is heated in an expansible vessel.
Question 3.
A cube with side 100cm at 00C is heated to 1000C. If the side becomes 101cm long find,
(a) The linear expansivity
(b) The cubic expansivity
Solution
(a) L1 = 100cm = 1m, L2 = 101cm = 1.01m, θ2 = 100o, θ1 = 0o
γ=increase in volumeoriginal volume×temperature rise=V2–V1V1(θ2–θ1)γ=1.01–11×100=0.01100=0.0001/k=1.0×10−4/k
(b) γ=3αγ=3×1.0×10−4=3.0×10−4/k
Apparatus: Thermometer, Density bottle, Retort stand, Water, Source of heat, Beaker, Beam balance, Liquid, Stirrer.
Method:
(i) Dry the density bottle and weigh it (M).
(ii) Fill the density bottle with the liquid that the apparent cubic expansivity is required and weigh it (M1)
(iii) Immerse the density bottle into a beaker of water and suspend with a thread on the clamp of the retort stand.
(iv) Take the original temperature of the water in the beaker (θ1).
(v) Heat the set up gently until the water boils.
(vi) Some liquid are expelled through the orifice of the bottle cover, the heating continues until no liquid is seen expelled again.
(vii) The final temperature of water is taken (θ2)
(viii) The density bottle is removed and wiped dry and re-weighed (M2).
Calculation
Mass of empty density bottle = M
Mass of density bottle + liquid = M1
Original temperature of water = θ1
Final temperature of liquid = θ2
Mass of remaining liquid + density bottle = M2
γα=Mass of liquid expelledMass of liquid remaining×temperature rise=M1–M2M2–M(θ2–θ1)
Conclusion
Since all the parameters are known, apparent cubic expansivity can be calculated.
EVALUATION
(i) Fire alarm
(ii) Bi-metallic thermometer
(iii) Temperature regulator in electric pressing iron
It consists of two different metals joined together. They expand at different rates when heated e.g brass and iron.
Application:
Steel plates and girders which are used in ship building and other constructional works are usually riveted together.
The large driving wheels of locomotive are fixed with steel tyre which are renewed from time to time as they wear out. In order to ensure a tight fitting, the tyre is made slightly smaller in diameter than the wheel. The tyre contracts on cooling thus ensuring tight fitting.
A tight glass stopper can be removed by standing the bottle in hot water. The glass bottle expands and the stopper becomes loose.
GENERAL EVALUATION
WEEKEND ASSIGNMENT
Read our disclaimer.
AD: Take Free online baptism course: Preachi.com 