Alternating Current AC Circuits

An a.c. circuit is one in which the magnitude of the current changes periodically with time. The a.c. is produced by an alternating voltage supply. The pattern of the a.c. voltage is sinusoidal in nature, that is it varies like the sine curve with constant amplitude and frequency.

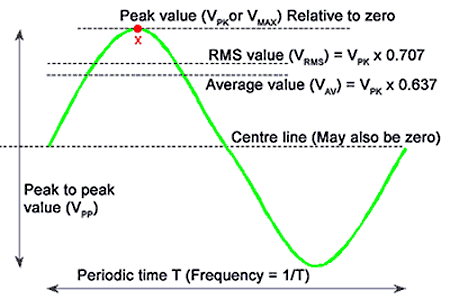
V₀ is the maximum or peak voltage, which represent the maximum displacement (amplitude).

V is the instantaneous voltage, representing the displacement.

Now, sinθ=VV0

Hence, V=V0sinθ=V0sinωt

The rms voltage is defined as the steady voltage which would produce the same heating effect per  second in a given resistor.

The rms value of current is defined as the steady current which would dissipate at the same rate in  a given resistor.

V0=2Vrms−−−−−√∴V=2Vrmssinωt−−−−−−−−−√

Thus, V=2(Vrmssin2πft)−−−−−−−−−−−−√

Where ω = 2πf

Similarly,

I=I0sinθ=2(Irmssinωt)−−−−−−−−−−√I=2(Irmssin2πft)−−−−−−−−−−−−√I0=Irms2–√

Where:

V : Instantaneous value

V₀: Peak value

V_rms : root mean square value.

Also,

I: Instantaneous value

I₀ : peak value

I_rms : root mean square value.

θ: phase angle between voltage and current

ω: angular velocity

A.C. in Resistors

The ability of a resistor to restrict the flow of current in an a.c circuit is called its resistance R.

When an a.c is applied to a resistor, both current and the voltage attain maximum and minimum at  the same time. Hence, they are in phase.

According to Ohm’s law,

R=VII0=V0RIrms=VrmsR

EVALUATION (POST YOUR ANSWERS USING THE QUESTION BOX BELOW FOR EVALUATION AND DISCUSSION):

1. Define an alternating current.
2. Describe the path of an a.c.
3. State the mathematical relationship between I₀ and I_rms.