Number bases

Number Base is a system of counting natural numbers in bundles. Some languages have their own unique method or way of counting numbers while others have same method. For instance, numbers are counted in bundle of ten digits called base ten or denary.  The digits involved in English natural numbers are: 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9.

Some unique number bases include: Base 2 ( Binary), Base 8 (Octal), Base 10 (Denary or Decimal), Base 16 (Hexadecimal),… there are other bases such as base 3, base 4, base 5, base 6, etc. The bases of number systems are usually written as a subscript either in word or figure. Examples: 111011₂ or 111011_two, 5734₈ or 5734_eight, 781₁₀ or 781_ten, etc.

NOTE: Numbers in base ten can be written without the base indicated. Therefore any number base that is written without base indicated should be considered as denary or base ten numbers.

CLASS ACTIVITY:

Teacher should ask the students to count in their mother tongues.

BINARY NUMBERS.

Binary numbers are system of counting numbers in base two. In binary system, the greatest digit is 1 and the least or lowest is 0. Hence, the two digits available in binary numbers are 1 and 0. Binary numbers is the most important number bases because of its usage in computer. Examples of binary numbers are 11111₂, 1000001_two, 0101₂, etc.

EXPRESSING BINARY AS SUM OF MULTIPLES

We can easily express any binary number as power of multiples of two as shown in the following examples.

CLASS ACTIVITY

Express each of the following as multiples of power of its base

(1)   1011_two        (2)  11000110_two       (3)  832_ten        (4)  890.701_ten

(5)100.1001_two   (6)   4302.42_six                      (7)  0.0247_eight

CONVERSION OF BINARY NUMBERS TO DECIMAL NUMBERS

To express binary numbers in decimals or denary, we write the binary number as a sum of multiples of powers of two, or we multiply each digit by  the base and add to the next digit starting from the left.

NOTE: Any number or letter raised to the power of zero is 1

Examples:

1. Convert 1111_two to denary scale.

Solution:

2.      Express 11101_two as a decimal number

Solution:

3.    Convert 1111110_two to a number in base ten.

Solution:

CLASS ACTIVITY

Express the following binary numbers as denary numbers.

1. 110111_two 1010101010_two                    3. 10000000101_two

CONVERSION OF OTHER NUMBER BASES TO DENARY

Converting other number bases to denary is the same as that of binary discussed earlier. Let’s study the examples below.

CLASS ACTIVITY

Express in denary the following number bases:

1. 124_eight 25_seven         3. 48_nine           4. 211_five

CONVERSION FROM DENARY TO ANY BASE

In converting a denary number to base two (binary) or any other base, we divide by that new base keeping the remainder in each step until there is nothing more to divide. The result is the list of remainders from the last to the first.

Example:                    

1. Convert 41_ten to base five
2. Convert 243_ten to base eight
3. Express 26₁₀ as binary number

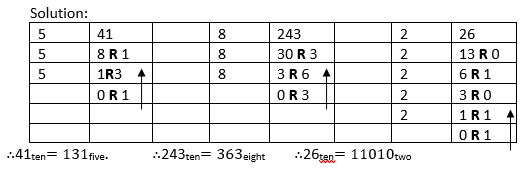
CLASS ACTIVITY

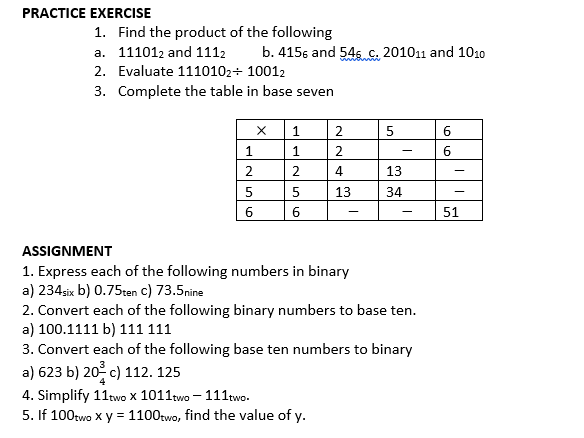
Convert the following base ten numbers to the base indicated in bracket in front of each.

1. 344(base 7) 3256(base 5)           c. 7054(base 6)            d. 106(base 2)

CONVERTING FROM ONE BASE TO ANOTHER BASE OTHER THAN BASE 10

To do this, two steps are involved:

Step1: convert the given base to base ten.

Step2: convert the result gotten from step1 above to the required base.

Example:

1. Convert 10111_two to base 6

CLASS ACTIVITY

Convert: (a) 405₆ to a binary number   (b) 321₄ to octal scale (c) 654₈ to base three.

BICIMAL NUMBERS.

Bicimals are binary numbers in fractional form in which the denominator is a power of 2. Examples include 10.101₂, 0.111₂, 1011.1101₂, etc.

CONVERSION OF BICIMAL TO DENARY

In converting bicimal numbers to denary, we write the bicimal numbers as a sum of multiples of powers of two. The whole numbers parts of bicimal are raised to positive power of 2 increasing to the left starting with zero. While the fractional part are raised to negative power of 2 decreasing to the left starting with negative 1 .

NOTE: Other bases in fractional form other than bicimal can also be expressed in denary using the same method as in bicimal. Teacher should teach the students using the repeated method of converting number bases to base ten (denary).

EVALUATION:

Convert each of the following to denary scale.

101. 1011₂ 3256₈           c. 101.101₂      d. 43.21₈          e. 32.21₅          f. 532₉.

ARITHMETIC OPERATIONS IN NUMBER

Basic operations of addition, subtraction, multiplication and division are carried out in other bases exactly the same as base 10.

ADDITION IN BINARY SYSTEM

To add in binary number, the following steps are important:

1. Arrange the numbers as in the addition of decimal numbers.
2. Add the elements of the column starting with the right most column.
3. Divide the sum by two.
4. Record the remainder, which is either 0 or 1.
5. Add the quotient to the sum of the next column and repeat the process for the next column.

ADDITION IN OTHER BASES:

The same principle applied when performing addition in binary and denary is applicable here also.

Examples:

1. Add 40002_five to 3403_five

NOTE: Your Teacher should solve more examples that includes adding in different bases, addition with missing numbers or digit in diferent bases.

CLASS ACTIVITY

Evaluate the following:

1. 1011_{2 2}
2. 100_{2 2} 10111₂

SUBTRACTION IN BASE TWO AND OTHER BASES

Subtractions in binary numbers are the same as subtraction in denary numbers. When the digit of the number to be subtracted is larger than the corresponding digit above it, we transfer one 2 from the next left column. If the immediate next column has zero digit, the transfer will be from further left column. The same principle is applicable to other bases other than base 2.

Your Teacher should explain this technique used in examples3 and 4 above with more examples.

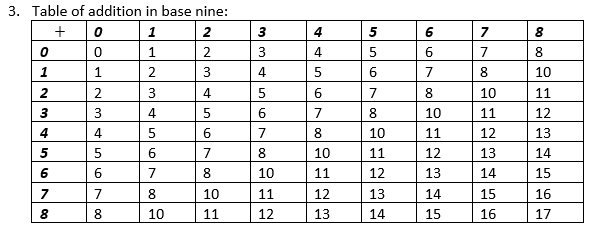
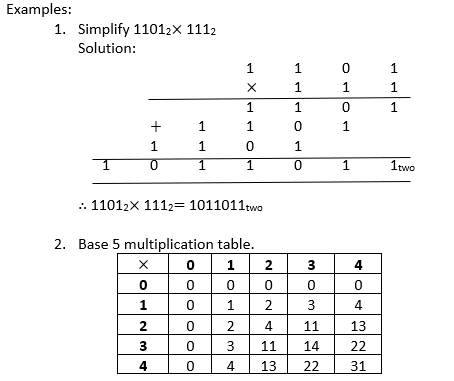
MULTIPLICATION AND DIVISION OF NUMBER BASES

MULTIPLICATION is a repeated addition. This principle is always applied while multiplying binary numbers and other number bases. The important thing we must note is that if we are working in base two and other bases, all the figures we use in the working should be less than 2 or the number base under consideration.