Chemical reaction rate refers to one or more of the following:
The units of reaction rate are (moles / dm3) / second. Different chemical reactions take place at different rates. The study of reaction rates is the study of the forming and breaking of chemical bonds.
The nature of the reactants involved in a chemical reaction will determine the kind of bonding that occurs.
Because of electron cloud repulsion, most neutral molecules that come in contact with one another bounce off without reacting. For these molecules to react, they must collide with enough kinetic energy to cause changes in the electron clouds of both molecules. When such a change occurs, an activated complex is formed, which allows the reaction to proceed. The energy required to give molecules enough kinetic energy to form an activated complex is known as the activation energy for the reaction.
Other factors affecting reaction rate:
Stable compounds do not spontaneously decompose in air.
However, the reaction takes place so slowly, at room temperature, that no observable change takes place for years. Since the rate of change is imperceptible, the substance is still considered stable.
Unstable compounds spontaneously decompose in air. The reaction takes place at such a rate that the change is observable.
A rate expression is a mathematical equation used to calculate the rate of a chemical reaction.
The rate expression for a reaction is expressed as k times the product of the concentrations of the reactants.
r a t e = k [ a ] [ b ]
If a chemical reaction occurs in one step, the concentrations of the reactants in the rate expression have exponents equal to the coefficients of the reactants in the balanced equation for the reaction.
If a chemical reaction occurs in more than one step, the concentrations of the reactants in the rate determining step (the step that has the slowest reaction rate) are the only ones that are important.
rate = k [H2O2] [HI]
This shows that the reaction occurs in more than one step
| Reactions where a single species falls apart in some way are slightly simpler because you won’t be involved in worrying about the orientation of collisions. Reactions involving collisions between more than two species are going to be extremely uncommon (see below). Reactions involving collisions between two species It is pretty obvious that if you have a situation involving two species they can only react together if they come into contact with each other. They first have to collide, and then they may react. Why “may react”? It isn’t enough for the two species to collide – they have to collide the right way around, and they have to collide with enough energy for bonds to break. (The chances of all this happening if your reaction needed a collision involving more than 2 particles are remote. All three (or more) particles would have to arrive at exactly the same point in space at the same time, with everything lined up exactly right, and having enough energy to react. That’s not likely to happen very often!) The orientation of collision Consider a simple reaction involving a collision between two molecules – ethene, CH2=CH2, and hydrogen chloride, HCl, for example. These react to give chloroethane. |
As a result of the collision between the two molecules, the double bond between the two carbons is converted into a single bond. A hydrogen atom gets attached to one of the carbons and a chlorine atom to the other.
The reaction can only happen if the hydrogen end of the H-Cl bond approaches the carbon-carbon double bond. Any other collision between the two molecules doesn’t work. The two simply bounce off each other.

Of the collisions shown in the diagram, only collision 1 may possibly lead on to a reaction
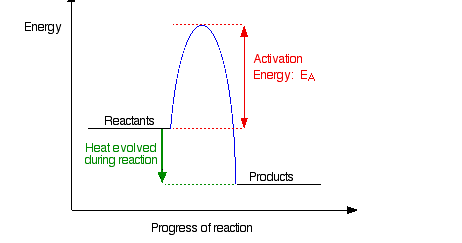
Note: The only difference if the reaction was endothermic would be the relative positions of the reactants and products lines. For an endothermic change, the products would have a higher energy than the reactants, and so the green arrow would be pointing upwards. It makes no difference to the discussion about the activation energy.
If the particles collide with less energy than the activation energy, nothing important happens. They bounce apart. You can think of the activation energy as a barrier to the reaction. Only those collisions which have energies equal to or greater than the activation energy result in a reaction.
Any chemical reaction results in the breaking of some bonds (needing energy) and the making of new ones (releasing energy). Obviously some bonds have to be broken before new ones can be made. Activation energy is involved in breaking some of the original bonds.
Where collisions are relatively gentle, there isn’t enough energy available to start the bond-breaking process, and so the particles don’t react.
The rate of reactions is influenced by the following factors:
(i) Concentration of the reactants,
(ii) Temperature of the reactants,
(iii) Particle size and nature of the reacting substances,
(iv) Presence of catalyst, and
(v) Exposure to radiations.
When a chemical reaction occurs, the reactants change over to products. It is observed that with the passage of time the concentrations of reactants decrease while those of products increase. It is graphically shown in Fig. 20.8.
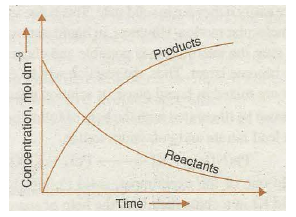
Fig. 20.8. Time dependence of the concentrations of reactants and products in a reaction.
Now, if we assume that other factors are constant then the rate of a chemical reaction decreases with the decrease in concentration of the reactants. For example, we find that a piece of’ wood bums at a much faster rate in oxygen than in air. It is because of higher concentration of O2 in the fanner.
Cato Guldberg and Peter Waage proposed a qualitative relationship between the rates of reactions and the concentration of the reacting species. This generalisation is known as ”Law of Mass Action”. It states that:
At a given temperature, the rate of a chemical reaction is directly proportional to the product of molar concentrations of reacting species with each concentration term raised to the power equal to numerical coefficient of that species in the chemical equation.
Thus, for a hypothetical reaction;
A + B à Produces
The rate according to law of mass action is given as Rate of reaction
where [A] and [B) are the molar concentrations of the reactants A and B respectively and k is a constant of proportionality.
Particle Size and Nature of Reactants
It is commonly observed that the nature of the reacting substances has a marked influence on the reaction rates. The effect of the nature of reactants can be described in terms of the following factors:
(a) Physical state of reactants
(b) Surface area and particle size of reactants
(c) Chemical nature of reactants.
(a) Physical State of the Reactants
We know that the chemical reaction takes place as a result of the collisions between the reacting particles. In order to collide with one another, the reacting particles must come close and intermix. Now intermixing of reacting particles cannot take place easily if they are in solid state. This is due to restriction in their molecular motion. However, in liquid state as well as in gaseous state the intermixing is possible and chances of their collision become larger. Thus, the reaction will be faster if the reactants are mixed in liquid phase or solution phase.
This can be illustrated with the help of following reaction between lead nitrate and potassium iodide.
Pb (NO3)2 + KI à PbI2 + KNO3
(i) In one of the experiment, solid Pb(NO3)2 is mixed with solid KI in a china dish with the help of spatula.
(ii) In another experiment, aqueous solution of Pb(NO3)2 is mixed with aqueous solution of KI in a beaker.

It is observed that rate of formation of ( yellow coloured Pbl2 is much faster in the second experiment because probability of encoumers between the- reacting particles is much larger in liquid phase than that in solid phase.
(b) Surface Area and Particle Size of Reactants
Particle size and surface area play an important role in rates of heterogeneous reactions particularly when one of reacting species is in .solid phase. Smaller the size of the reacting particles present in the solid phase larger will be their surface area. As a result, more will be the probability of the reacting species coming in contact with each other and therefore, more will be the .number of encounters between them. For example,
(c) Chemical Nature of the Reactants
The chemical nature of reacting substances also affects the reaction rates significantly. Depending upon the nature of reacting species, the rates of different reactions may differ very widely from one another. For example, the oxidation of ferrous ions (Fe+2) by potassium permanganate in acidic medium is practically instantaneous. Whereas oxidation of oxalate ions (C2O 4– 2) by potassium permanganate in acidic solution is comparatively much slower:
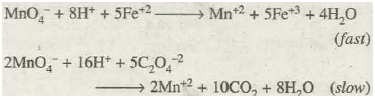
In these two reactions, everything is identical except the nature of reducing agents.
The change in pressure also affects the rate of a reaction.
In doing rate experiments with a solid and solution reactant e.g., marble chips-acid solution or a solid catalyst like manganese(IV) oxide catalysing the decomposition of hydrogen peroxide solution, it is sometimes forgotten that stirring the mixture is ail important rate factor.
Reactions carried out in the presence of light radiations are known as photochemical reactions. The presence/absence of radiations greatly affects the rate of a reaction. Some examples are given below to illustrate the idea.
Photosynthesis in green plants occurs in the presence of sunlight. The green chlorophyll molecules absorb the photon energy packets of sunlight and initiate the chemical changes summarised below:
Water + carbon dioxide à glucose + oxygen
6H2O(l) + 6CO2(g) à C6H12O6(aq) + 6O2(g)
The rates of almost all reactions increase with the increase in temperature. For example,
In most of the cases it has been found that the rate of the reaction becomes almost double for every 10° rise of temperature. This is also expressed in the terms of Temperature coefficient which is the ratio of rate constants of the reaction at two temperatures differing by 10°. The two temperatures generally selected are 298 K and 308 K.
Thus,
Temperature coefficient = Rate constant of 308 K / Rate constant at 298 K
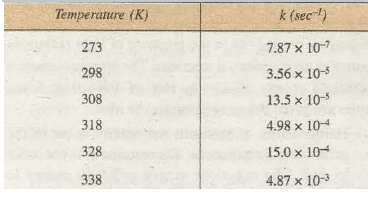
The rate constants for the decomposition of N2O5 at different temperatures is given in Table 20.1. From the table, it is seen that rate constant at 273 K is 7.87 x w-1 and at 298 K is 3.56 X w-5 This shows that for 25° rise of temperature of the rate constant increases by 43 times.
Table 20.1. Rate Constants for the Decomposition of N2O 5 at Different Temperatures
Home → Experiment to Show How Changes in Temperature Affect the Rate of a Reaction
Kids, do you think that temperature will have an affect on how fast or slow a reaction might take place? In order for a chemical reaction to occur, the molecules, which are reactants, must physically come into contact with one another. Anything that increases the frequency of these encounters will increases the rate at which products are formed. Your hypothesis can be that the rate of a chemical reaction will be increased by raising the temperature of reactants.
Requirement
Six clear cups, a measuring cup, a thermometer (-20°C to 110°C), three original formula effervescent Alka-Seltzer® tablets, a stopwatch, a mortar and pestle, a source of hot water, ice cubes, and graph paper.
Procedure
Fill a clear glass with exactly 50 cm3 of hot water. Use the thermometer to take the temperature and record it on a data sheet. Drop 1 Alka-Seltzer® tablet into water. Measure the time required for the tablet to fully dissolve. Be prepared to start and stop on time. The reaction will take less than 15 seconds. Record the time. Repeat this experiment using room temperature water.
For the cold water test, the procedure is a little different. Fill a clear glass with 25 crn3 of water and add enough ice to adjust the level to 50 cm3. Stir the ice water for about 15 seconds so the temperature will come to equilibrium. Use the thermometer to take the temperature and record it on your data sheet. (Leave the ice cubes in the water!) Drop 1 Alka Seltzer tablet into the water. Measure and record the time required for the reaction to be completed.
Analysis
Graph your data points (water temperature vs. time to fully dissolve) to show the effect of temperature on rate of reaction.
Home → Analysis and Interpretation of Simple Graphs on Rates of Reaction
Graph 1 shows the decrease in the amount of a solid reactant with time. The graph is curved, becoming less steep because the reactants are being used up, so the speed decreases. In the first few minutes the graph will (i) decline less steeply for larger ‘lumps’ and (ii) decline more steeply with a fine powder o time (min) i.e., (i) less surface area gives slower reaction and (ii) more surface area a faster reaction.
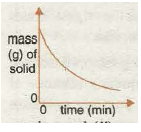
Graph 2 shows the increase in the amount of a solid product with time. The graph tends towards a maximum amount possible when all the solid reactant is used up and the graph becomes horizontal. This means the speed has become zero as the reaction has stopped.
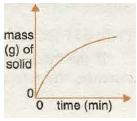
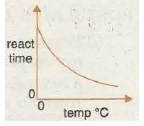
Graph 3 shows the decrease in reaction time with increase in temperature as the reaction speeds up. The reaction time can represent how long it takes to form a fixed amount of gas in the first few minutes of a metal carbonate-acid reaction, or the time it takes for so much sulphur to form In tin sodium thiosulphate-hydrochloric acid reaction
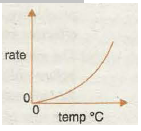
Graph 4 shows the increase in speed of a reaction with increase in temperature as the particles have more and more kinetic energy. The rate of reaction is proportional to lit, where tis the reaction time
Graph 5 shows the increase in the amount of a gas formed in a reaction with time. Again, the graph becomes horizontal as the reaction stops when one of the reactants is all used up!
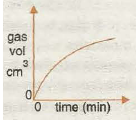
Graph 6 shows the effect of Increasing concentration, which decreases the reaction time, as the speed increases because the greater the concentration the greater the chance of fruitful collision.
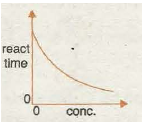
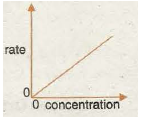
Graph 7 shows the rate/speed of reaction is often proportional to the concentration of one particular reactant. Rate This is due to the chance of a fruitful collision forming products being proportional to the concentration
Home → Collision Theory of Reaction Rates
Collision theory, was developed by Max Trautz and William Lewis in 1916-18 and, provides a greater insight into the energetic and mechanistic aspects of reactions and their rates. According to this theory, the reactant molecules are assumed to be hard spheres and reaction can occur when molecules collide with each other. The number of collisions per second per unit volume of the reaction mixture is known as collision frequency (Z). The more frequent are collisions, the faster is the reaction.
POSTULATES OF COLLISION THEORY
(i) Reactions occur due to approach and collisions of reactant particles (atoms, molecules or ions) .
(ii) A successful collisions, the one required for changing reactants to products, can occur between two molecules only if they possess a certain minimum amount of energy in excess of the normal energy of molecules.
(iii) Only a small fraction of collisions are successful in producing a reaction. These collisions are called effective collisions.
(iv) The minimum energy which molecules must possess before collision should be equal to or greater than the activation energy.
(v) The rate of reaction is proportional to the frequency of effective collisions per second.
It must be noted here that the collisions between reactant molecules will not lead to reaction even if the energy requirement is satisfied. It is because the colliding molecules should also have proper orientation.
Proper Orientation:

Improper Orientation:
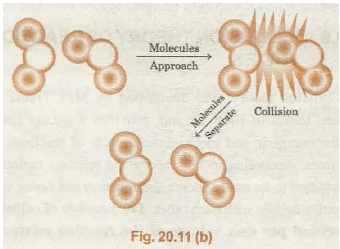
The proper orientation of reactants molecules leads to bond formation whereas improper orientation make them simply bounce back and no products are formed.
A pictorial representation (Fig. 20.11(n) .and 20.11 (b)) is shown, to illustrate the above idea.
An extension of the collision theory is the activated complex or transition state theory. In the activated. complex theory:
1. When two molecules or species approach each other, their electron clouds repel and distort each other. The potential energy of the reactants rises and reaches a maximum value, forming a combined and highly unstable molecule called the activated complex.
2. When the activated complex loses energy it can either form products or break down to form the original reactants. The activated complex is described as being in the transition state.
3. The energy required to from the activated complex is known as the activated energy barrier, and it is only reacting molecules which have greater energy than the activation energy barrier which ‘climb’ over to form the products (Fig. 20.11).
Collision Theory and Reaction Rate
Reactions can happen only when the reactant particles collide. All the collisions which occur are not successful in forming product molecules. The reason is that particles have a wide range of kinetic energy but only a small fraction of particles have enough kinetic energy to break bonds and bring about chemical change. The minimum kinetic energy required for reaction is known as the activation energy.
The small number of high kinetic energy collisions between particles which do produce a chemical change are called ‘fruitful _collisions’. Here the reactant molecules collide with enough kinetic energy to break the original bonds and form new bonds in the product molecules.
It must be noted that the rate-controlling factors described below are to do with the collision frequency (chance of collision) or the energy of reactant particle collision (energy activation energy) which can summed up as the ‘chance of a fruitful collision’ leading to product formation.
THE EFFECT OF CONCENTRATION
If the concentration of any reactant in a solution is increase, the rate of reaction is increase. Increasing the concentration, increases the probability of a collision between reactant particles because there are more of them in the same volume and so increases the chance of a fruitful collision forming products.
For example, Increasing the concentration of acid molecules in a reaction of zinc with HCl, increase the frequency or chance at which they hit the surface of marble chips to dissolve them faster.
THE EFFECT OF TEMPERATURE
When gases or liquids are heated the particles gain kinetic energy and move faster (see diagrams below.) The increased speed increases the chance (frequency) if collision between reactant molecules and the rate increases.
It must be noted that this is not the main reason for the increased reaction speed, so be careful in your theory explanations if investigating the effect of temperature.
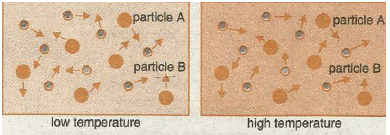
THE EFFECT OF SURFACE AREA-PARTICLE SIZE OF A SOLID REACTANT
If a solid reactant or a solid catalyst is broken down into smaller pieces the rate of reaction increases.
The speed increase happens because smaller pieces of the same mass of solid have a greater surface area compared to larger pieces of the solid.
Therefore, there is more chance that a reactant particle will hit the solid surface and react.
Role of Activation Energy in Chemical Reactions
A reaction can occur when molecules of reactants collide with each other to form an unstable intermediate (Fig. 20.12). The intermediate exists for a very short time and then breaks up to form product molecules. The energy required to form this intermediate, called activated complex (C), is known as activation energy (E a). The distribution of kinetic energy of different fraction (NE/NT) of molecules is shown in Fig. 20.12.
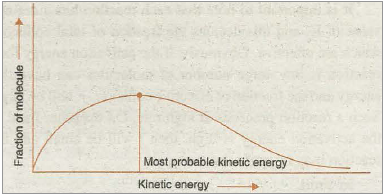
Fig. 20.12. Distribution curve showing energies among gaseous molecules.
Only those collisions result in the formation of products which possess energy equal to or more than the certain minimum energy called threshold energy. Collisions of the molecules possessing energy less than threshold energy do not form products. It means that between reactants and products there is an energy barrier which must be crossed before the reactants are converted into products. The energy required for crossing this energy barrier is supplied by the kinetic energy of the -molecules.
“The minimum extra energy over and above the average potential energy of the reactants which must be supplied to the reactants to enable them to cross over the energy barrier between reactants and products is called Activation energy”. Thus,
Activation energy= (Threshold energy) – (Average energy of the reactants)
or E a = E y-E R
The idea of activation energy and the energy barrier involved in a reaction is given in the Fig. 20.13.
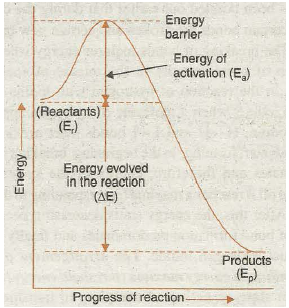
Fig. 20.13. Illustration of activation energy and energy barrier involved in a reaction.
It is important to note that each reaction has a definite value of Ea and this decides the fraction of total collisions which are effective. Obviously, if the activation energy for a reaction is low, large number of molecules can have this energy and the fraction of effective collision, J, will be large. Such a reaction proceeds at high rate. On the other hand, if the activation energy is high, then f will be small and the reaction may be quite slow.
In short,
For fast reactions; activation energies are low.
For slow reactions; activation energies are high.
For example, for the reaction between NO and O2, Ea is low and hence, reaction is fast whereas for the reaction between CO and O2, Ea is high and hence, the reaction is slow.
2NO + O2 à 2NO2
2CO + O2 à 2CO2
The two theories can be successfully used to explain how the factors of surface area, concentration or pressure of gases, temperature and catalysts affect reaction rates.
In the case of surface area, concentration and pressure of gases at constant temperature, any increase in any individual value is equivalent to an increase in the number of molecules colliding per second. An increase in the frequency of effective collisions results in an increase in reaction rate.
ACTIVATED COMPLEX OR TRANSITION STATE THEORY
It has been pointed out earlier that during the chemical reaction certain bonds are broken and certain new bonds are formed. The breaking of bonds requires energy whereas the formation of bonds results in the release of energy. For example, in the reaction of hydrogen with iodine to form hydrogen iodine, when a molecule of hydrogen approaches that of iodine, H-H and I- I bonds start breaking and H- I bonds start forming. In the beginning, breaking of bonds predominates and therefore, energy of the system starts increasing till it reaches a maxima (corresponding to threshold energy). After this, the energy starts decreasing because the process of bond· formation predominates and finally leads to the product hydrogen iodide. The arrangement of atoms corresponding to energy 11UlXima (threshold energy) is called transition state or activated complex. In transition state, the system has partial reactant character and partial product character as shown in Fig. 20.14 and Fig. 20.15.
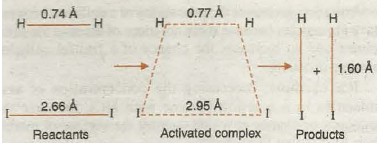
Fig. 20.14. Formation of activated complex during the reaction of H2 and I2 from HI.

Fig. 20.15. Transition state or activated complex.
The difference between energy of the transition state and energy of the reactants is equal to activation energy.
E transition state – E reactants = E activation
Effect of Temperature and Catalyst on the Rate Constant
Let us now consider the effect of increase in temperature on the number of effective collisions.
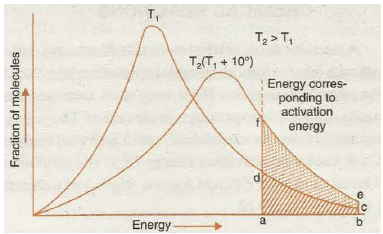
Fig. 20.16. Energy distribution at different temperatures
On the basis of probability consideration Fig. 20.16 is drawn to give the energy distribution curves at temperatures T1 and T2 (where T 2 = T 1 + 1 0). Now as we know that the rise in temperature increases the kinetic energy of molecules ( ·: K.E. T) therefore, the energy distribution curve gets flattened and shifts towards higher energy region. A close examination of the curves in the graph clearly reveals that the function of molecules possessing higher kinetic energy, i.e., energy greater than threshold energy, as indicated by shaded portion becomes almost double and therefore the rate of reaction almost doubles for 10 rise of temperature. Thus, increase in the rate of reaction with increase in temperature is mainly due to increase in number of collisions which are energetically effective.
Temperature Dependence of Rate Constant
Arrhenius developed the mathematical relation between temperature and the rate constant on the basis of the observations from the large number of experiments. This temperature dependence of the rate constants is expressed algebraically as
K = A e-E a /RT
Equation (20.1) is called Arrhenius equation. Here A is pre exponential factor and is called frequency factor, Ea is the energy of activation and Tis the temperature in kelvin scale.
The term e -Ea I RT in the above equation is also called as Boltzmann Factor. Both A and E0 are characteristic of the reaction. Another form of the equation which is more useful for calculations is obtained by taking logarithm of Eqn. (20.1), therefore,
Log k2 / k1 = Ea / 2.303 R [ 1/T1 – 1 / T2]
Here k2 and k1 are rate constant at temperature T1 and T2 respectively Ea is activation energy and R is universal gas constant.
EFFECT OF CATALYST ON RATE OF REACTION
A catalyst is a substance that alters the rate of chemical reaction without itself being permanently chemically changed. Never state things like “it doesn’t react, just speeds it up”. It must take part in the reaction and it must change chemically, albeit on a temporary basis. A catalyst provides a different ‘pathway’ ormechanism that makes the bond breaking processes (or other electronic changes in the reactants) occur more readily. In general,
Thus, the function of a catalyst is thus to lower down the activation energy. In sample words, greater the decrease in the activation energy caused by the catalyst, higher will be the reaction rate. In the presence of a catalyst, the reaction follows a path of lower activation energy. Under this condition, a large number of reacting molecules are able to cross-over the energy barrier and thus the rate of reaction increases. The energy profile diagram for the catalysed and uncatalysed reactions are as shown in the Fig. 20.17. Where dotted curve represents the progress of uncatalysed reaction and solid curve represents:- the catalysed reaction.
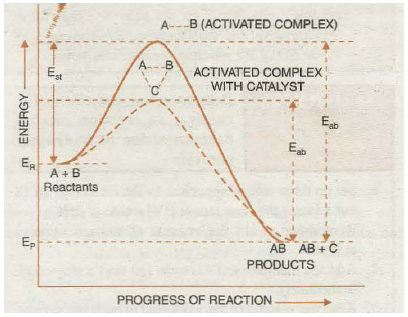
Fig. 20.17. Potential energy curves for catalysed and uncatalysed reactions.
For a general reaction of the type A + B à AB the course of uncatalysed and catalysed reaction may be represented as:
(a) Uncatalysed reaction:
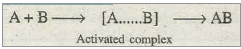
(b) Catalysed reaction:
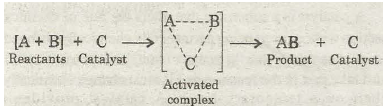
Though the catalyst increases the rate of the reaction, yet it does not effect the state of equilibrium in case of reversible reactions. It is because the activation energy for the forward reaction and backward reaction is reduced to the same extent.
EVALUATION
2.If 2g of zinc granules was reacted with excess dilute HCl to evolve hydrogen gas which came to completion after 5minutes.Calculate the rate of the chemical reaction in g|hr.
3.Which of the following lowers the activation energy of a chemical reaction
a.water b .freezing mixture c.catalyst d.reducing agent.
4.Which of the following will not affect a chemical system at equilibrium?
a.Temperature b. catalyst c. pressure d.concentration
| 5. An increase in the rate of a chemical reaction on heating is due to increase in a.activation energy b.enthalpy c.collision rate d .reactant concentration 6.A catalyst a.increase the amount of product in an equilibrium mixture b.only affects gaseous reaction c.must be used in small quantities THEORY 1.State all the factors that affect the rate of a reaction 2.Explain how any three of these factors affect the rate of a chemical reaction 3.State the collision Theory. 4.Define Activation Energy. (post your answers on the forum for review) |
Read our disclaimer.
AD: Take Free online baptism course: Preachi.com 