When an a.c is applied through a capacitor, current leads by 90° or π2radians. They are out of phase.
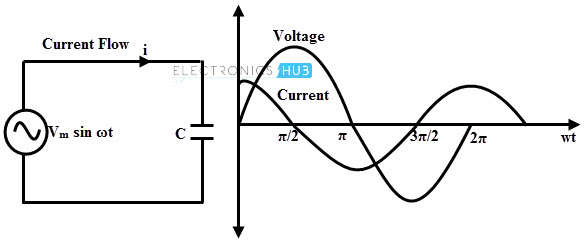
The ability of a capacitor to resist the flow of current in an a.c circuit is called its ‘Capacitive Reactance Xc’.
The reactance of a capacitor, Xc is given by:
XC=1ωC=12πfCIrms=VrmsXCandI0=V0XC
The capacitance of a capacitor is measured in Farad F.
A.C. Through an Inductor
When an a.c is applied through an inductor, voltage leads by 90° or π2radians. They are out of phase.
An inductor has an inductance (L), measured in Henri (H). The ability of an inductor to restrict the flow of current in an a.c circuit is called its ‘Inductive Reactance Xl’. The reactance of an inductor, Xl is given by:
XI=ωL=2πfLIrms=VrmsXLandI0=V0XL
Worked Examples
Example 1:
A capacitor of 1μF is used in a radio circuit where the frequency is 1000Hz and the current is 2mA. Calculate the voltage across the capacitor.
Solution:
V=IXC
But, XC=12πfC
Also, I=2mA=21000=0.002AV=I2πfC=0.0022π×1000×1×10−6=0.32V
(NB: μ = 10– 6, m= 10– 3)
Example 2:
An inductor of 2H and a negligible resistor is connected to 12V mains supply. If the frequency is 50Hz, find the current flowing.
Solution:
I=VXL=122πfL=122π×50×2=628.3A
Series Circuits
1. Capacitor and resistor in series (RC circuit):
When a capacitor is connected in series with a resistor, the total opposition to the current flowing through the circuit is called ‘Impedance, Z’. Here, current leads voltage by 90°. From the vector diagram above,
V2=V2C+V2R∴V2=I2X2C+I2R2V2I2=X2C+R2
But Z=VI→Z2=V2I2∴Z2=X2C+R2∴Z=X2C+R2−−−−−−−√
For the phase angle,
Tanθ=VCVR=IXCIR=XCR
2. Inductor and resistor in series:

When an inductor is connected in series with a resistor, voltage leads by 90° on the current.
Considering the vector diagram,
V2=V2L+V2R∴V2=I2X2L+I2R2V2I2=X2L+R2
But Z=VI→Z2=V2I2∴Z2=X2L+R2∴Z=X2L+R2−−−−−−−√
For the phase angle,
Tanθ=VLVR=IXLIR=XLR
3. Capacitor, inductor and resistor in series (RLC Circuit):

Now, V2=V2R+(VL−VC)2V2=I2R2+(IXL−IXC)2V2=I2R2+I2(XL−XC)2V2I2=R2+(XL−XC)2Z=(R2+(XL−XC)2)−−−−−−−−−−−−−−−−√
Note that the two reactance must be subtracted before squaring.
For the phase angle,
Tanθ=VL−VCVR=XL−XCR
Worked Examples
Example 3:
A 2.5μH inductor is connected in series with a non-inductive resistor of 300Ω across a 50V alternating at 160Hz. Calculate the r.m.s value of the current in the circuit.
Solution:
Vrms=IrmsZIrms=VrmsZ
Now, Z=X2L+R2−−−−−−−√
But, XL=2πfL=2π160×2.5×10−6=2.5×10−3ΩZ=3002+(2.5×10−3)2−−−−−−−−−−−−−−−−√=300ΩIrms=50300=0.17A
Example 4:
A 2.0μF capacitor is connected in series with a resistor of 300Ω across a 240V a.c alternating at 160Hz. Find the rms value of the current in the circuit.
Solution:
Irms=VrmsZ
Now, Z=X2C+R2−−−−−−−√
But, XC=12πfL=12π160×2.0×10−6=497.4Ω∴Z=3002+(497.4)2−−−−−−−−−−−−√=580.8ΩIrms=240580.8=0.41A
EVALUATION (POST YOUR ANSWERS USING THE QUESTION BOX BELOW FOR EVALUATION AND DISCUSSION):
- State the mathematical relationship between Z, XC and XL.
- Define an impedance Z.
- Define the reactance of a capacitor and an inductor.
Read our disclaimer.
AD: Take Free online baptism course: Preachi.com 