Definition of a Capacitor
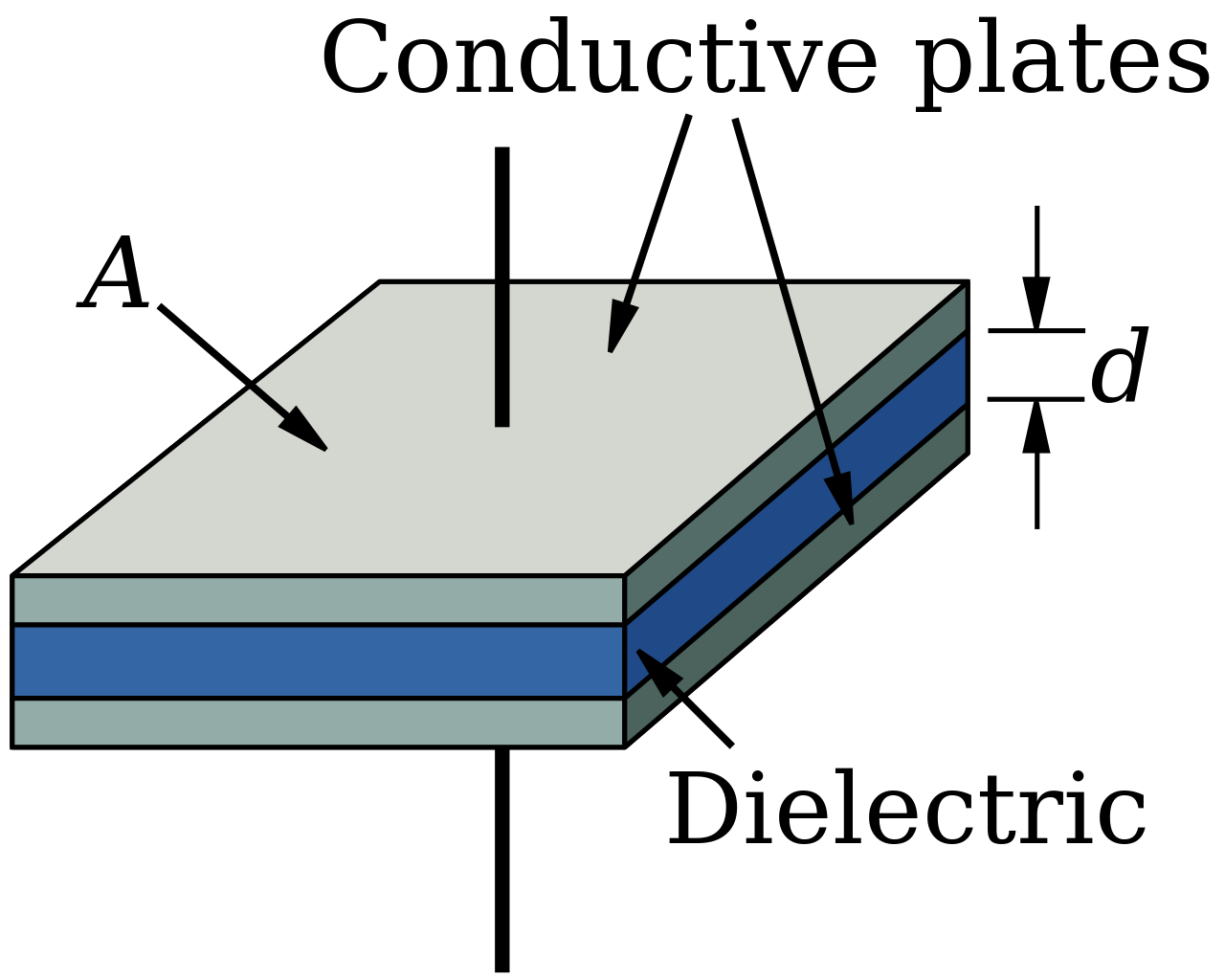
A capacitor can be defined as a device which can store electrical energy. It consist essentially of two metal plate separated by an insulator. The insulator is called dielectric material. When the capacitor is connected to a pd source, opposite charges are gradually built up on each of the plates.

The ratio of the charge Q stored on the capacitor to the potential difference between the plates is called the capacitance of the capacitor. The unit of capacitance is called farad.
C=QV ——–(i)
Q is the charge and V is the pd between the plate.
The most common type of capacitor is the parallel plate capacitor. The capacitance of a parallel plate capacitor depends on the following factors:
(i) Area of overlap of the plates: the capacitance of a parallel plate capacitor is directly proportional to the area of overlap of the plates.
C∝A
(ii) Distance between the plates: the capacitance of the parallel plate capacitor is inversely proportional to the distance between the plate.
C∝1d
(iii) Dielectric constant of the insulator between the plates: the capacitance of the capacitor is directly proportional to the dielectric constant of the insulator. The dielectric constant is the permittivity of the insulator to electric line of flux.
C∝ε
Summarily the capacitance of the capacitor is given as:
C=εAd ——–(ii)
EVALUATION (POST YOUR ANSWERS USING THE QUESTION BOX BELOW FOR EVALUATION AND DISCUSSION):
- What is meant by a dielectric substance?
- List the factors which determine the capacitance of a parallel plate capacitor and state the effect of each of them has on the capacitance.
- Explain what is meant by the statement, ‘the capacitance of a capacitor is 5µF’
Energy Stored in a Capacitor
A capacitor stores electrical energy. When the capacitor is connected to a pd source, the charge on it plate built up gradually from zero to Q. The work done is charge with an average voltage is :
W=12QVW=12CV2W=1Q22C——–(iii)
The charging and the discharging process for a capacitor is given below:

Arrangement of Capacitors
Capacitors can be arrangement in a circuit in parallel or in series.
Series Arrangement
Here, the capacitors are connected end to end as shown below.

For capacitors in series;
(i) Equal charge Q will be stored in the capacitor.
Q1=Q2=Q3
(ii) The sum of the potential difference across each plate is equal to the potential difference supplied by the source.
V=V1+V2+V3
but,
C=QV
Hence, V=QC
Substituting this into the expression for V,
QC=QC1+QC2+QC3
Cancelling Q out,
1C=1C1+1C2+1C3 ——–(iv)
The reciprocal of the equivalent capacitance for capacitor in series is equal to the sum of the reciprocal of the individual capacitors in the series.
Parallel Arrangement
Here, capacitors are arranged as shown below.

For capacitor in parallel,
(i) The potential difference across the plates of the capacitor is equal.
V=V1=V2=V3
(ii) The total charge stored is the sum of all the charged stored in each capacitor.
Q=Q1+Q2+Q3
but,
C=QV
Hence, Q=CV
substituting this into the expression for Q,
CV=C1V+C2V+C3VC=C1+C2+C3——–(v)
The equivalent capacitance for capacitors in parallel is the sum of capacitance for the individual capacitor.
Solved Questions
- A work of 30 J is done to transfer 5 mC of charge from a point B to a point A in an electric The potential between B and A is
Solution:
Charge Q = 5 mC
Work = 30J
Note that W = QV
V=WQ=305×10−3=6000V
- A capacitor of capacitance 3.0µF is subjected to a 2000 V potential difference across its Calculate the energy stored in the capacitor
Solution:
Capacitance C = 3.0µF
Potential difference V = 2000V
Energy E =?
Recall that E=12CV2E=3.0×10−6×600022E=54J
- A series arrangement of three capacitors of value 8µF, 12µF and 24µF is connected in series with a 90V battery.
(i) Draw an open circuit diagram for this arrangement
(ii) Calculate the effective capacitance in the circuit
(iii) On close circuit, calculate the charge on each capacitor when fully charged
(iv) Determine the voltage across the 8µF
Solution:

- For capacitors in series, effective capacitance is given as:
1C=1C1+1C2+1C31C=18+112+124=3+2+1241C=624
Taking the reciprocal of both sides,
C1=246
Effective capacitance C=4µF
- Recall for capacitors in series,
The charge stored on each capacitor is equal
Q=CVQ=4µ×90Q=4×10−6×90Q=3.6×10−4C
- Recall, Q=CVV=QCV=3.6×10−48×10−6V=0.45×102=45V
The voltage across the 8µF capacitor is 45V
EVALUATION (POST YOUR ANSWERS USING THE QUESTION BOX BELOW FOR EVALUATION AND DISCUSSION):
- The plate of a parallel plate capacitor, 5.0 x 10-3m apart are maintained at a potential difference of 5.0 x 104calculate the magnitude of the:
- electric field intensity between the plate
- force on the electron
- acceleration of the electron
(Electronic charge = -1.6 x 10-19C, mass of electron = 9.1 x 10-31kg)
- A capacitor of capacitance 3.0µF is subjected to a 200V potential difference. Calculate the energy stored in the capacitor
Read our disclaimer.
AD: Take Free online baptism course: Preachi.com 