NUMBER BASES
In Mathematics, a base or radix is the number of different digits or combination of digits and letters that a system of counting uses to represent numbers. For example, the most common base used today is the decimal system. Because “dec” means 10, it uses the 10 digits from 0 to 9. Most people think that we most often use base 10 because we have 10 fingers.
A base can be any whole number bigger than 0 (if it was 0, then there would be no digits). The base of a number may be written next to the number: for instance, 23 8 {\displaystyle 23_{8}\ } 238 means 23 in base 8 (which is equal to 19 in base 10).
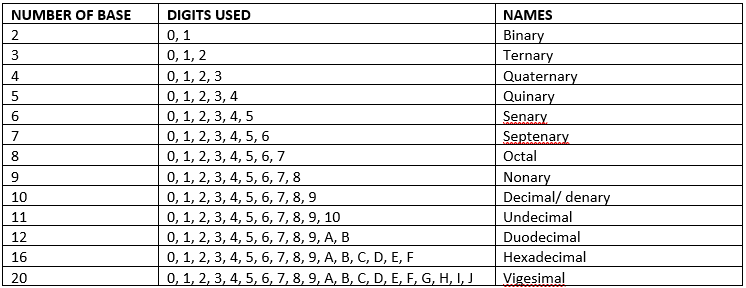
The popularity of the base 2, 8 and 16 is because of its use in modern technology.
COUNTING IN GROUPS OF TWOS (BINARY)
A Binary Number is made up of only 0s and 1s. An example is 110100
There is no 2, 3, 4, 5, 6, 7, 8 or 9 in Binary! A “bit” is a single binary digit. The number above has 6 bits.
Binary numbers have many uses in Mathematics and beyond. In fact the digital world uses binary digits.
To show that a number is a binary number, follow it with a little 2 like this: 1012. This way people won’t think it is the decimal number “101” (one hundred and one).
How do we Count using Binary?
| Binary | ||||||
| 0 | We start at 0 | |||||
| 1 | Then 1 | |||||
| ??? | But then there is no symbol for 2 … what do we do? | |||||
| Well how do we count in Decimal? | ||||||
| 0 | Start at 0 | |||||
| … | Count 1,2,3,4,5,6,7,8, and then… | |||||
| 9 | This is the last digit in Decimal | |||||
| 10 | So we start back at 0 again, but add 1 on the left | |||||
The same thing is done in binary.
| Binary | |||||||
| 0 | Start at 0 | ||||||
| 1 | Then 1 | ||||||
| 10 | Now start back at 0 again, but add 1 on the left | ||||||
| 11 | 1 more | ||||||
| ??? | But NOW what? | ||||||
| What happens in Decimal? | |||||||
| 99 | When we run out of digits, we … | ||||||
| 100 | … start back at 0 again, but add 1 on the left | ||||||
And that is what we do in binary.
| Binary | |||
| 0 | Start at 0 | ||
| 1 | Then 1 | ||
| 10 | Start back at 0 again, but add 1 on the left | ||
| 11 | |||
| 100 | start back at 0 again, and add one to the number on the left… … but that number is already at 1 so it also goes back to 0 … … and 1 is added to the next position on the left | ||
| 101 | |||
| 110 | |||
| 111 | |||
| 1000 | Start back at 0 again (for all 3 digits), add 1 on the left | ||
| 1001 |
Here are some equivalent values:

Binary numbers also have a beautiful and elegant pattern

BINARY PLACE VALUES (POSITION)
In the Decimal System there are Ones, Tens, Hundreds, etc
In Binary there are Ones, Twos, Fours, etc, like this:

Numbers in base 10 are sometimes referred to as Decimal Numbers or Denary. Decimal numbers can be converted to binary numbers by dividing the number repeatedly by 2 and the remainders written on the right column until the last number is zero (0).

CONVERTING NUMBERS IN BASE 2 TO BASE 10
When binary number are expressed as a sum of multiple of power of two ,the sum of the values of those powers is a number in base ten . Hence, to convert numbers in base two (binary number ) to numbers in base ten , we express the numbers as sums of multiples of two.
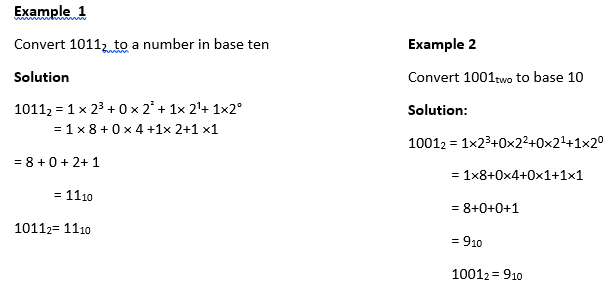
ASSIGNMENT
Convert the following base ten numbers into binary
Convert the following base ten numbers into binary
What is the last digit of:

Read our disclaimer.
AD: Take Free online baptism course: Preachi.com 