The numbers used in multiplication have special names as illustrated below:
141(factor) x 17 (factor) = 2397 (product)
The product is a multiple of each of the factors, i.e.
2397 is a multiple of 141
2397 is a multiple of 17
Multiplication is a short way of writing repeated additions. For example,
3 x 4 = 3 lots of 4
= 4 + 4 + 4
= 12
With directed numbers,
(+4) + (+4) + (+4) = 3 lots of (+4)
= 3 X (+4)
The multiplier is 3. It is positive. Thus,
(+3) X (+4) = (+4) + (+4) + (+4) = +12
(+3) X (+4)
1 X (+4)

The illustration above shows 1 x (+4) and (+3) x (+4) as movement on the number line. The movements are in the same direction from 0.
Similarly,
(-2)+ (-2) + (-2) + (-2) + (-2)
= 5 lots of (-2)
= 5 X (-2)
The multiplier is 5. It is positive.
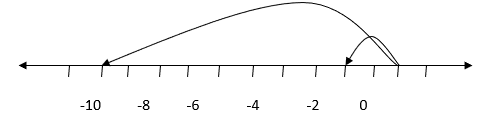
Thus, (+5) x (-2)
= (-2) + (-2) + (-2) + (-2) + (-2)
= -10
This is illustrated below:
In general, (+a) x (+b) = + (a x b)
(+a) x (-b) = – (a x b)
(-a) x (-b) = + (a x b)
Examples 1:
Negative multiplier
In general: (-a) x (-b) = -(a x b)
(-a) x (-b) = + (a x b)
Examples 2
Simplify the following:
CLASS ACTIVITY:

Division of whole numbers
Division by a number, e.g., 4 is best considered as multiplication by 1/4, and then we can use the results for the multiplication that we have established. Thus,
+8 ÷ (+2) = + 1/2 x (+8) = + 4
-8 ÷ (+2) = + 1/2 x (-8) = -4
+8 ÷ (-2) = – 1/2 x (+8) = -4
-8 ÷ (-2) = – 1/2 x (-8) = +4
In general: (+a) (-b) = – (a
(-a) (-b) = + (a
Examples:
Simplify the following:
Solutions:
Since 2 x (+4) +8,
Then 5 + 8 =13
First, (-3 + (-5)) = -3-5 = -8
Therefore, (-3 + (-5)) ÷ (-2) = -8 ÷ -2
= + (8 ÷ 2) = 4
= (6 + 8) ÷ (-4)
= 14 ÷ (-4)
= – (14 ÷ 4)
= -31/2
CLASS ACIVITY:
Simplify the following:
Read our disclaimer.
AD: Take Free online baptism course: Preachi.com 