area of shapes

Diameter = 2r, where r= radius

Example: 

1. Find the area of a circle whose radius is 3½m. (Take π to be ²²⁄₇)

Solution:

Area of a circle = πr²

227×(312)2=227×72×72=11×72=772m2=38.5m2

2. The area of a circle is 126.5cm². Find its radius correct to 2 decimal places.

Solution:

Area of circle = πr²

126.5cm2=227r22532=227r2253×7=22×2×r2r2=1614r=1614−−−√r=12.6892r=6.345r=6.35(2d.p.)

Area of a Triangle

Any diagonal of a rectangle divided it into two equal right- angled triangles forms a right angled triangle.

Thus:

Area of a right – angled triangle

= ½ × product of sides containing the right angle.

Area of triangle = ½ × base × height.

Example:

Calculate the area of the triangle shown below

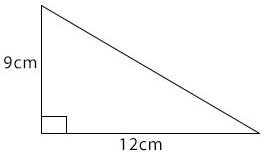
The two sides containing the right angle measure 9 cm and 12cm.

Area of triangle = ½ × 9cm × 12cm

= 54cm²

2. Calculate the height of a triangle whose base and area is 8cm and 20cm²respectively.

Solution:

Area of triangle = ½ × base × height

20cm² = ½ × 8cm × h

20cm² = 4hcm

h = 20cm²/4cm

h = 5cm.

Therefore, height of the triangle = 5 cm.

CLASS ACTIVITY

1. Using π = 22/7, calculate the area of a circle whose diameter is 21m.
2. Find the base of a triangle whose area is 270cm² and height 18cm.

Area of a Square

A square is a shape whose length and breadth are equal

Area of a square = l² = (length of side)²

Therefore, length of side = area of square−−−−−−−−−−−√

Solution:

Area of triangle = ½ × base × height

20cm² = ½ × 8cm × h

20cm² = 4hcm

h = 20cm²/4cm

h = 5cm.

Therefore, height of the triangle = 5 cm.

CLASS ACTIVITY

1. Using π = 22/7, calculate the area of a circle whose diameter is 21m.
2. Find the base of a triangle whose area is 270cm² and height 18cm.

Area of a Square

A square is a shape whose length and breadth are equal

Area of a square = l² = (length of side)²

Therefore, length of side = area of square−−−−−−−−−−−√

Examples:

1. Find the area of a square whose side is 5cm.

Solution:

Formula for area of a square = l²

= 5cm × 5cm

= 25cm²

2. The area of a square field is 100m², find the length of its side.

Solution:

Length of side = area of square−−−−−−−−−−−√=100m2−−−−−√=10m

Area of a Rectangle

A rectangle 5cm long by 3cm broad can be divided into squares of side 1cm as shown below.

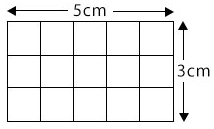
By counting, the area of the rectangle = 15cm².

Notice also that 5 × 3 = 15. Thus in general;

Area of rectangle = length × breadth.

Also notice that 5 = 15 ÷ 3 and 3 = 15 ÷ 5

Hence,

Length of rectangle = area ÷ breadth

Breadth of rectangle = area ÷ length

Examples:

1. Calculate the area of rectangle 6cm by 3.5cm

Solution:

Area of a rectangle = length × breadth

= 6cm × 3.5cm

= 21 cm

2. The area of a rectangle is 224cm². If its length is 16cm, calculate the breadth.

Solution:

Breadth = arealength=22416cm=14cm

Area of a Parallelogram

The area of the parallelogram, P = area of rectangle, R

= b×h

In the diagram above, the height of the parallelogram is h and its base is b.

In general,

Area of parallelogram = base × height

Base of parallelogram = area ÷ height

Height of parallelogram = area × base

Area of a Trapezium

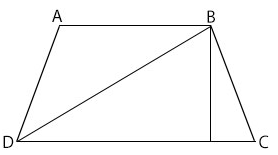
ABCD is a trapezium in which AB is parallel to DC. The diagonal AD divides the trapezium into two triangles. The height, h, is the same for both triangles.

area of trapezium ABCD

= area of Δ ABD + area of Δ BDC

=  ½ AB × h + ½ DC × h

= ½ (AB + DC)h

Example:

Calculate the area of the trapezium ABCD in figure below

The diagonal AC divides the trapezium into two triangles. The height of each triangle is 8 cm.

Area of Δ ACB = ½ × 13cm × 8cm =52cm²

Area of Δ ACD = ½ × 6cm × 8cm = 24cm²

Area of trapezium = 52cm² + 24cm² = 76cm²

CLASS ACTIVITY

1. Copy and complete the tables of rectangles below

2. A floor 4m long and 3½ m wide is to be concreted. Find the (a) area of the floor (b) the cost, if concrete costs ₦200 per m².

Area of Irregular Shapes

Example:

1. Calculate the area of the shape below. All measurements are in meters and all angles are in right angles.

Solution:

The shape can be split into a 3 × 3 square and 6 × 10 and 2 × 4 rectangles.

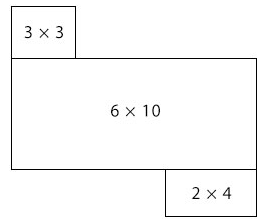
Area = area of square + area of the 2 rectangles = (3 × 3 +6 × 10 + 2 × 4 )m²

= (9 + 60 + 8)m²

= 77 m²

PRACTICE EXERCISES

1. The area of a parallelogram is 20cm², the base is 16cm. Find its height.
2. Ada has a small square garden of 250cm. What is its area in m²?
3. Find the area of a circle whose circumference is 154cm
4. The area of a trapezium is 81cm² and its height is 6cm. Find the longer side if the shorter side is 11cm.
5. Find the area of a tank which measures 25cm by 10cm.

ASSIGNMENT

1. 1. Find the area of a circular disc of diameter 28cn
2. Calculate the area of parallelogram whose base is 6cm and height is 2.5cm
3. Obtain the area of trapezium whose lengths of parallel sides are 3cm and 7cm and height is 6cm.
4. The adjacent sides of a parallelogram are 16cm and 12cm. If the height corresponding to the base 12cm is 8cm, calculate: (a) the area of parallelogram (b) the height corresponding to the base 16cm.