Plane shapes

A flat surface, such as top of a table, a playing field, ceiling, wall, face of a tin and star board face is referred to as a plane. It is a plane because it is two dimensional, i.e. it is measured in only two directions.

Figures drawn on flat or plane surfaces are called plane shapes. Examples include rectangle, square, triangle, parallelogram and trapezium.

All these shapes are referred to as a regular shape, i.e. they have definite length and breadth.

There are also irregular shapes (they do not have definite length and breadth), e.g. leaves, stones, etc.

Circle

The shape traced out in which every point of it is same distance from a fixed centre point is called circle.

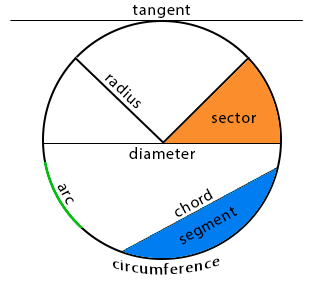
The outer –boundary of the circle is called the circumference. The curved part of the circumference is called arc.The radius is the straight line joining the centre to any part on the circumference.

The straight line that divides the circle into semicircles is called the diameter. The line that divides the circle into two segments is called the chord.

The region bounded by the diameter and the arcs of a circle is called the semi-circle. The sector is the region bounded by two radii and the arc of the circle. The segment is the region bounded by the chord and the arc of the circle. A circle has infinite number of lines of symmetry.

CLASS ACTIVITY

1. How many lines of symmetry have a circle?
2. Describe the following parts of a circle (a) radius (b) sector (c) segment (d) chord (e) diameter.

Triangles

Definition of Triangle

A triangle is a closed figure made up of three line segments.

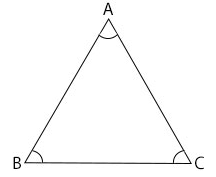
A triangle consists of three line segments and three angles.

Basic Properties of Triangles

1. The sum of the angles in a triangle is 180°. This is called the angle-sum property.
2. The sum of the lengths of any two sides of a triangle is greater than the length of the third side. Similarly, the difference between the lengths of any two sides of a triangle is less than the length of the third side.
3. The side opposite to the largest angle is the longest side of the triangle and the side opposite to the smallest angle is the shortest side of the triangle.

In the figure above, ∠B is the largest angle and the side opposite to it (hypotenuse), is the largest side of the triangle

Types of Triangles Based on Sides

Equilateral Triangle

A triangle having all the three sides of equal length is an equilateral triangle.

Since all sides are equal, all angles are equal too. It has three lines of symmetry.

Isosceles Triangle

A triangle having two sides of equal length is an Isosceles triangle.

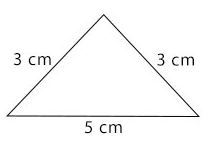
The two angles opposite to the equal sides are equal. It has one line of symmetry.

Scalene Triangle

A triangle having three sides of different lengths is called a scalene triangle

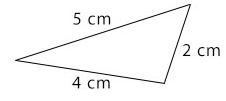
A scalene triangle has no line of symmetry.

Types of Triangles Based on Angles

Acute-angled Triangle

A triangle whose all angles are acute is called an acute-angled triangle or acute triangle.

Obtuse-angled Triangle

A triangle whose one angle is obtuse is an obtuse-angled triangle or Obtuse triangle

Right-angled Triangle

A triangle whose one angle is a right-angle is a right-angled triangle or right triangle.

CLASS ACTIVITY

1. How many lines of symmetry have a) an equilateral triangle b) a scalene triangle?
2. List three basic properties of triangle.

Properties of Quadrilaterals

Square

Properties of a Square

(i) All the four sides and angles are equal.

(ii) All corners of a square are identical and each equal to right angle.

(iii) Each pair of opposite sides of square is parallel and equal.

(iv) The diagonal of a square are equal and they bisect each other at point of intersection.

(v) A square has four lines of symmetry. They are line passing through the point of intersection of the diagonals.

Rectangle

Properties of a Rectangle

(i) The two opposite sides of a rectangle are equal

(ii) All corners of a rectangle are identical and each equal to right angle

(iii) Each pair of opposite sides of rectangle is parallel and equal

(iv) The diagonal of a rectangle are equal and they bisect each other at point of intersection

(v) A rectangle has two lines of symmetry. They are line passing through the point of intersection of the diagonals.

Trapezium

A trapezium is a quadrilateral having two opposite sides parallel while the others are not.

Properties of Trapezium

(i) The two opposite side are parallel while the other two are not

(ii) The total angle in a trapezium is add up to 360°

(iii) It has no line of symmetry

Parallelogram

In a parallelogram, opposite sides are equal and parallel.

Properties of a Parallelogram

(i) The diagonals of a parallelogram bisect each other.

(ii) A parallelogram has rotational symmetry of order 2.

(ii) Parallelogram has no line of symmetry.

Rhombus

A rhombus is a parallelogram with four equal sides.

Properties of a Rhombus

(i) The diagonals of a rhombus bisect each other at right angles.

(ii) A rhombus has two lines of symmetry and it has rotational symmetry of order 2.

Kite

A kite has two pairs of adjacent sides of equal length.

Properties of a Kite

(i) The diagonals of a kite cross at right angles.

(ii) A kite has one line of symmetry.

The Quadrilateral Family Tree

CLASS ACTIVITY

1. How many lines of symmetry do the following have?

(a) a rectangle (b) a circle (c) a square

2. How many triangles are there in the diagram below?

Identification and Naming of Polygons

Definition of Polygon

A polygon is a 2-D shape made when line segments enclose a region.

2-D stands for two-dimensional. These two dimensions are length and width. Polygons have no thickness.

The line segments are called sides.

An endpoint is called a vertex. Together they are called vertices