Three dimensional shapes

Identification and Naming of Solids

Solid figures are often called 3-dimensional shapes or 3D shapes. A solid figure is simply anything that occupies space and also has a definite shape. Most solids, or 3D shapes, such as stones and trees, have rough and irregular shapes. However, some solids, such as boxes, tins, football, etc. have regular shapes. These are often called geometrical solids

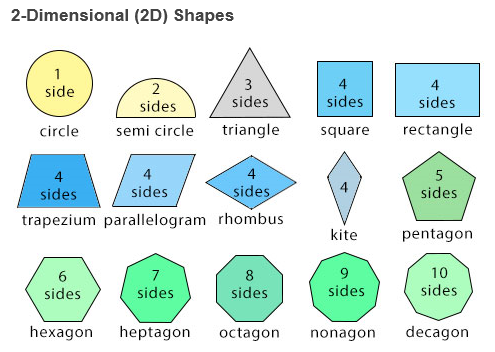
3-Dimensional (3D) Shapes

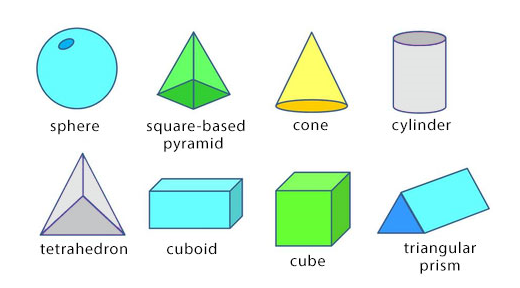
Basic Properties of Prisms

A prism is a solid figure with ends. It has base and top (opposite) faces that are parallel and are of the same size and shape. Its sides have opposite edges that are equal and parallel. The common prisms are cubes, cuboids and cylinders. Other are named after the shape of their top and bottom faces e.g. a prism with a triangle as its base is a triangular based prism, etc.

A face (f) is any plane surface that makes up prism.

An edge (E) is a line where two faces meet. it may be straight or curved.

A vertex (V) is a point or corner where three or more edges meet. The plural of vertex is vertices.

A prism with n-sides has the following properties:

(i) n + 2 number of faces

(ii) 3n edges

(iii) 2n vertices

Basic Properties of a Cube

Examples: A cube of sugar, maggi cube, dice, etc.

Properties of a Cube

1. A cube is a special cuboids which has all its edges (sides) equal in length.
2. They have 6 equal faces in the shape of a shape.
3. Cubes have 12 edges.
4. They have 8 vertices.

Basic Properties of Pyramids and Cones

Properties of a Pyramid

A pyramid is a solid figure whose base is a polygon and whose lateral faces (surfaces) are triangles with a common vertex called a pyramid. Pyramids are classified according to their bases and named after the shape of their bases e.g. a pyramid with a triangle as its base is a triangular based pyramid, etc

Basic Properties of a Cone

Examples: Sharpened point of a crayon or pencil, mound of groundnut, ice-cream, etc.

Properties of a Cone

1. A cone has only one vertex
2. A circular edge.
3. One curved surface
4. A circular flat face
5. A cone has two faces

Basic Properties of a Sphere

Examples: A ball, table tennis egg, etc.

Properties of a Sphere

1. It has only one spherical face in its entire surface.
2. It has no edges and no vertex.

Nets of Solids

Nets of a Cube

Net of a Cuboid

The Volume of Cubes and Cuboids
The volume of a solid is a measure of the amount of space it occupies. The cube is used as the basic shape to estimate the volume of a solid. Therefore, volume is measured in cubic units.
The Volume of a Cube
If one edge of a cube is s unit long, then
Volume of a cube = side × side × side
i.e. V = s × s × s
= s3
Worked Examples:
1. Calculate the volume of a cube of an edge 4cm.
Solution:
Volume of a cube = length × height × width
= s × s × s
= 4 × 4 × 4
= 64 cm3
NOTE: The above formula can be used to find the edge of a cube when the volume is given.
S3 = V
S = V−−√3
e.g. A cube of volume of 27cm3 has an edge of
S = S−−√3 = 27−−√3
= 3×3×3−−−−−−−√3 = 3 cm
2. A container in the shape of a cube is used to store a liquid. One edge of the container is 25cm long. The depth of the liquid in the container is 15cm as shown in the diagram below.
(a) Calculate the volume of liquid in the container.
(b) Calculate the volume of the container not filled with liquid.

Solution:

(a) Base area of the container = 25 x 25 = 625cm²

Depth of liquid in the container = 15cm

Volume of liquid in the container = 625 x 15 = 9375cm³

(b) Volume of the cube = S³  = 25 x 25 x 25

= 15 625cm³

Volume of the container not filled liquid

= 15 625 – 9 375

= 6 250cm³

The Volume of a Cuboid

A cuboid is also called a rectangular prism. It has length, width (breadth) and height (thickness).

The volume of a cuboid = length × breadth × height

V =  l × b × h

The volume of the above solid is

V = 6 × 4 × 2 = 48cm³

Note: In the above formula, l × b = A. Where A = base area of the cuboid.

Hence: Volume of a cuboid = Area of base × height

= Area of any face × thickness of the face.

Worked Examples

1. A box has a square base of side 9cm. Calculate the volume of the box if it is 10cm deep.

Solution:

Volume of the box = Area of Square base × depth of the box

Area of Square base = 9cm × 9cm = 81cm²

Volume of the box = 81 × 10 = 810 cm³

2. A cuboid is 12cm long and 8cm wide as shown in the diagram below. If the volume of cuboid is 624cm³, find the height of the cuboid.

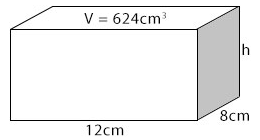
Solution:

Length × width × height = volume

i.e  l × w × h = V

Substituting V = 624cm³, l = 12cm  and  w = 8cm

12 × 8 × h = 624

96h = 624

h = 624/96 = 6.5cm

Hence, the height of the cuboid = 6.5cm.

CLASS ACTIVITY

1. A book measures 18cm by 12cm by 3cm. Calculate its volume.
2. The volume of a cube is given as 512cm³
3. What is the length of one edge of the cube?
4. How many small cubes of edge 2cm can be placed together to make this cube?
5. The base of a cuboid has one side equal to 10cm, and the other side is 5cm longer. If the height of the cuboid is 7cm, find the volume of the cuboid.
6. Calculate the volume of air in a dormitory 10cm long, 5m wide and 3m high.

PRACTICE QUESTIONS

1. Each of the cuboids in the figure below have the same volume. Find the missing lengths

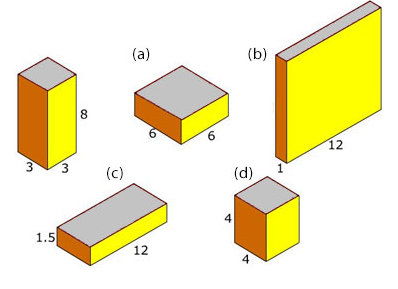
2. Find the volume of the cuboids in the image below